Global resource potential of seasonal pumped hydropower storage for energy and water storage

Global model

To assess the global potential of SPHS, our methodology integrates five critical components, which are: topography, river network and hydrology data, infrastructure cost estimation and project design optimization. SPHS project suitability mainly depends on the topography, distance to a river and water availability, which together determine the technical potential. Additional contextual factors, such as distance from energy demand and associated transmission infrastructure losses and associated costs, determine the economic feasibility. Whilst previous studies have used similarly high-resolution topography for conventional reservoir dams estimation¹⁶, the possibility of storing water and energy by pumping water to a reservoir parallel to a major river has not been globally assessed. Since storage potential and infrastructure costs are highly dependent on the topography, our new spatially explicit approach identifies numerous technically feasible candidate sites and provides estimates of costs.

Details of the SPHS world potential model framework are explained step-by-step in Fig. 3 and Supplementary Tables 3–5. The model goes through each grid cell location delineated at a 15″ resolution, implementing a detailed siting assessment that accounts for topography and hydrology in the calculation of project-level costs. The model performs the stages as follows. First, it looks for a river with reasonable flowrate up to 30 km away from a reservoir (Fig. 3c), second it checks if a dam up to 250 m high can be built from the grid cell (Fig. 3d), third it removes projects with competing dams (Fig. 3e), fourth it finds the flooded side of the dam and creates the reservoir (Fig. 3f), fifth it calculates the volume and flooded areas, sixth it compares the size of the storage site with the water available for storage (Fig. 3g), seventh it estimates the costs of the dam, tunnel, turbine, generator, excavation and land, eighth it estimates water and energy storage costs (Fig. 3i).

Fig. 3: Seasonal pumped hydropower storage (SPHS) world potential model framework.

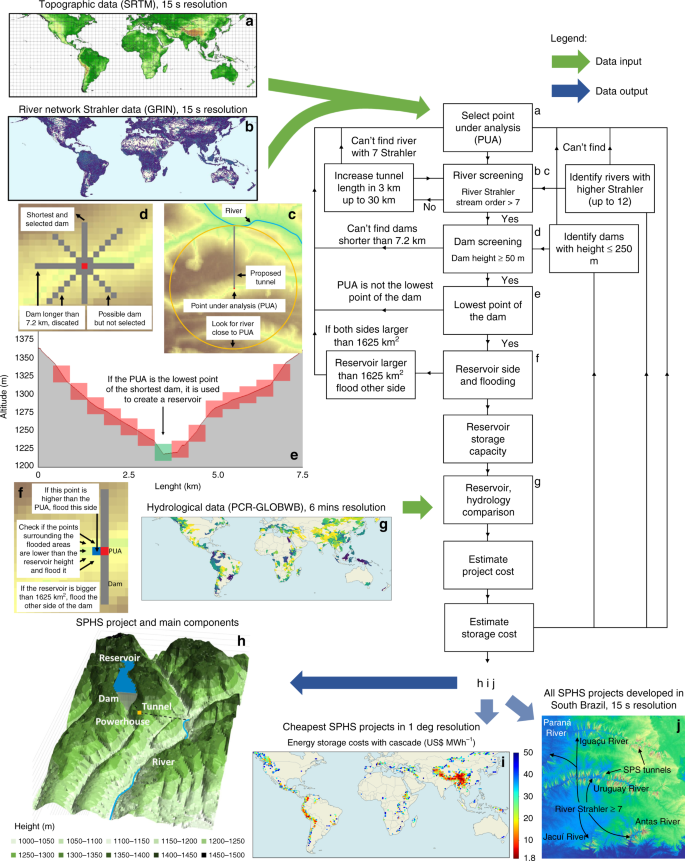
a Topographical data input from the Shuttle Radar Topography Mission (SRTM)³⁰. b River network Strahler data input from the Global River Network (GRIN)³¹. c Finding rivers close to the SPHS site. d Looking for possible dams. e Limiting the number of proposed SPHS projects. f Creating and finding reservoirs. g Hydrological data input³². h Representation of a possible SPHS project in the Zambezi river basin. i Cheapest SPHS projects in 1-degree resolution. j Location with several SPHS projects proposed.

Full size image

SPHS reservoirs in this study are operated to reduce the seasonality and interannual river flow variations, to regulate the flow of the river. If the river flow is already constant, then the water available for storage in the SPHS reservoir will be zero, as it would deregulate the flow of the river. The hydrological data were used to restrict the size of the storage reservoirs, according to water availability. This guarantees that there will be water available to fill up the storage reservoir without having a considerable impact on the overall river flow. Additionally, conservative storage values are assumed to reduce the impact of the SPHS plant in the river flow. The maximum volume of the reservoir equals to 11% of the annual river flow, from which the need for storage is divided by seasonal storage needs and inter-annual storage needs. This value was selected with the intent of reducing the environmental impact of storage on the overall river flow. On average, the water available for storage in SPHS reservoirs in this model equals to 7.7% of the annual river flow (Supplementary Fig. 1).

Data collection

The SPHS World Potential Model provides a near-global scale potential (56°S–60°N). The excluded area is due to unavailable Shuttle Radar Topography Mission (SRTM) topographic data. The topographic data applied is SRTM³⁰ and has 3″ resolution. The resolution is decreased to 15″, assuming the centre point, to reduce modelling time and to combine with the river network data. The river network data assumed the Strahler methodology in Global-scale river network (GRIN)³¹, which is derived from the SRTM data and has 15″ resolution. The topographic and river Strahler data are then combined with the hydrological data taken from the PCR-GLOBWB³² global hydrological model, which are derived into annual discharge, seasonal, and inter-annual variations. We use methods to optimize the number and diameter of the tunnels³³ and for cost-estimation³⁴ procedures, which are further explained in Supplementary Tables 2 and 3.

Site selection model and engineering design

The site selection model is divided into nine main stages (Supplementary Table 4). Initially, the topographic data are combined with the river Strahler data, which is a numerical measure of its branching complexity and was derived from the same topographic data. The higher the Strahler stream order value the more tributary rivers (branches) deliver water to the given part of the river³¹. The two are compared at the same resolution to identify rivers within the topographic data and to estimate the length of the tunnels connecting the upper reservoir and the lower reservoir in the river. The river Strahler data are also used to reduce the amount of SPHS projects developed within a given area and reduce the modelling time. Rivers with small river Strahler stream order have low river flows, which results in unviable SPHS projects with small generation capacities. A minimum river Strahler stream order of 7 is selected because the river has a considerable number of tributary rivers connected to it, which results in a relatively large and constant river flow.

For each land grid cell at a latitude between 60° N and 56° S (point under analysis (PUA)), the model searches for rivers with sufficient discharge (river Strahler stream order ≥7) within 1–30 km of distance, which consists of the tunnel length. If a large river is found, the model attempts to build dams of 50, 100, 150, 200 and 250 m height, along four axes (N–S, W–E, NW–SE, NE–SW) and with a maximum length of 7.2 km (Supplementary Table 4 (L4)). If the topography allows the construction of such dams, it verifies whether the PUA is the lowest point of the dam (if it is not, the process stops with the intention of not repeating the same project). Using the surrounding topography and observing limits to the maximum flooded area of the reservoir, the model identifies the side with the largest storage volume. Subsequently, the reservoir water level is varied to determine the flooded area vs. level and storage volume vs. level curves. This is done by subtracting the volume of land and water with the reservoir at a given level by the volume of land and water with the reservoir at its minimum level. Project costs are estimated using the equations presented in the ref. ³⁴. The cost is divided in dam, tunnel, powerhouse excavation, pump-turbine, electro-technical equipment and land costs. More details on the assumptions for the cost estimate are presented in Supplementary Table 3. In the analysis, the water storage capacity of the SPHS projects is limited according to the water availability of the main river. The maximum water storage capacity is limited to 11% of the annual river flow, which is a small portion of the river flow and results in a small impact to the river. If the storage capacity is much higher than the amount of water available, the estimated cost of storage increases, as a section of the reservoir will never fill up. The project costs are then compared with the hydrology of the river to find the water and energy storage costs with Eqs. (4) and (5).

Storage dimensioning and cost

The seasonal and interannual variability of river discharge used in the Hydrological Analysis Stage is calculated with the Eqs. (1) and (2). They are important to calculate the water available for storage in the SPHS reservoir, with the objective of producing a constant river flow. If the river has no seasonal variation, then the water available for storage would be equal to zero. This is because, if the SPHS deregulates the flow of the river, the hydropower potential of the dams in cascade or the water supply downstream could be negatively affected.

where, S_V is the seasonal variation index, I_V is the interannual variation index, (bar q_{mathrm{{m}}}) is the river flow of a given m month, (bar q_{mathrm{{y}}}) is the average river flow of a given year, (bar q_{mathrm{{s}}}) is the average river flow over y years, N_m is the number of months, N_y is the number of years.

The costs of water and energy storage services calculated in the Estimate Storage Cost stage vary according to the annual river flow, the seasonal and interannual variation indexes. These hydrological parameters have three main purposes. Firstly, they intend to guarantee that there will be sufficient water in the river to be stored in the upper reservoir. Secondly, the need for water and energy storage should not have a substantial detrimental impact on the river flow. Thirdly, the water storage potential intends to regulate the flow of the river and produce a constant flow of water, reducing its seasonality and interannual variations.

Using the values calculated for S_V and I_V (Supplementary Fig. 2) and the percentage of river annual discharge available for storage (Supplementary Fig. 1), the water available for storage Q_A (Eq. (3)) is calculated by

where Q_A is the water available for storage in km³ yr⁻¹, Q is the river annual discharge in km³ yr⁻¹.

The variation of the water and long-term energy storage costs with the water available for storage is presented in Eq. (4). The costs for additional short-term energy storage are presented in Eq. (5). For more details on Eqs. (1)–(5) please refer to the Supplementary Table 2.

where C_W is the cost of water storage in US$ km⁻³, C_P is the cost of the project (i.e. dam, tunnel, turbine, electrical equipment, excavation, and land) in US$, W_s is the water storage capacity adjusted by the water availability in km³, C_Ewoc is the cost of long-term energy storage excluding the cascade in US$ MWh⁻¹, C_Ewc is the cost of long-term energy storage including the cascade in US$ MWh⁻¹, W_R is the water storage capacity of the reservoir developed in the model in km³, E_Rwc and E_Rwoc are the energy storage capacity of the reservoir developed in the model with and without cascade in MWh, respectively.

where, C_GW is the cost of additional generation capacity in US$ kW⁻¹, C_PGW is the cost of additional generation capacity (i.e. tunnel, turbine, electrical equipment, excavation) in billion US$, G is the generation capacity in GW (fixed to be 1 GW for all SPHS plants proposed).

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Source: Resources - nature.com