Climate and hydrology
To assess the risk of low flows, large sets of climate timeseries were generated using the Weather@Home climate simulation system (W@H)28. W@H comprises an atmospheric global climate model, HadAM3P, and a regional climate model, HadRM3P, for generating dynamically downscaled projections, over the region of interest at 0.22° resolution (~25 km). W@H229 was adapted to produce 100 unique 30-year projections for three time slices: (i) one historical baseline (1975–2004); and two forced by the RCP 8.5 emission scenario (ii) NF (2020–2049) and (iii) FF (2070–2099). The outputs are mostly available at daily resolution, for 14 common climate variables including air temperature, bias-corrected precipitation, evaporation, wind speed, radiation, air pressure, soil moisture content and heat fluxes.
We used the hydrological model, DECIPHeR30, to simulate river flows from the W@H climate projections. DECIPHeR is a flexible hydrological modelling framework that explicitly characterises connectivity and fluxes across the landscape. It has previously been applied to 1366 gauges across Great Britain and shown to achieve good model performance in replicating hydrological behaviour across a range of catchments and flow conditions. DECIPHeR groups together similar parts of the landscape into hydrological response units (HRUs) to minimise run times of the model and enable it to run large ensembles of climate simulations and provide probabilistic flow simulations essential for risk analysis. In this study HRUs are classified by three classes of slope, accumulated area and the W@H climate grid to ensure the spatial variability of climatic inputs was represented. DECIPHeR was set up for 24 flow gauges located closest to the 32 power plants of interest (Supplementary Fig. 5). To calibrate the model, daily observed data of precipitation, potential evapotranspiration (PET) and discharge for a 30-year period from January 1, 1973 to December 31, 2003 were used to run and assess the model (Supplementary Fig. 1). National gridded 1 km2 estimates of rainfall and PET from the CEH gridded estimates of areal rainfall (CEH-GEAR; refs. 31,32) and CHESS-PE33 datasets were aggregated to the W@H grid and used to drive the model. For each gauge 10,000 parameter sets were sampled in a Monte Carlo simulation using wide parameter ranges tested in previous studies [13]. Model performance was evaluated against observed flow at each of the gauges from January 1, 1974 to December 31, 2003 using log Nash–Sutcliffe efficiency34 and root mean squared error, finding the former was best to reproduce flows below the 10th percentile flow (Q90), our flow range of interest (Fig. 7). To represent hydrological model uncertainty, we then used the 100 best performing parameterisations (1%) to simulate flows for each of the W@H climate timeseries. This resulted in a total of 720,000 30-year daily flow simulations, consisting of 100 hydrological model parameterizations for each of the 100 30-year W@H projections for three time slices and 24 gauges.
Power plant availability
We use a set of 32 power plants, all of which are thermo-electric (coal, combined cycle gas turbines, municipal and industrial waste incineration and biomass), water-dependent plants cooled by either evaporative or hybrid cooling systems using water from freshwater bodies and ranging in nameplate capacity between 35 and 2400 MWe (refs. 35,36, Supplementary Table 4, Supplementary Fig. 5). Power plant availability is calculated at each of 33 power plants on a daily basis, by comparing simulated flows from DECIPHeR at each gauge with the hands off flow reductions determined by the environmental flow requirements and sectoral allocations. The EU Water Framework Directive also regulates water temperatures, although these have minimal impact on water use for evaporative cooling (as opposed to once through cooling) and thus are not considered here. Likewise, coastal thermo-electric power plants are also not constrained by freshwater availability. The current system plus (CSP) soft hands off flow regulatory regime for withdrawals from freshwater bodies was simulated, as proposed by UK Government during the abstraction reform process37,38,39. CSP incorporates sectoral allocations and environmental flow requirements, as calculated in ref. 38, with 10–20% allocated for EFR at Q90 depending on the ecological sensitivity of the waterbody to abstraction38,40. If the no go below flow discharge is reached, typically set at 75% of the Q99.9, all abstraction must stop.
From Q90 and up to that point, sectoral (and individual user) allocations are incrementally reduced (hands off flows), such that at Q99, only 10% of a user’s normal allocation is available. Since power plants are unlikely to operate at less than 30% nameplate capacity, in effect a power plant’s availability becomes 0 when the flow hits Q97 (Supplementary Table 1). Figure 3c of the results illustrates how seemingly small plant-level impacts accumulate during more severe drought events that impact multiple units.
Supply curves
The UK electricity supply market is designed for competition to promote least-cost for the consumer. This means for each half hour period of every day, suppliers bid to fulfil the expected, albeit unknown, demand. The cheapest supply is contracted to fulfil the demand, where the supply curve intersects the demand curve, so suppliers who have bid too high will not be called upon to generate. The price of electricity paid to all suppliers is the most expensive successful bid, known as the strike price. Note that suppliers bid based on their short-run marginal cost (SRMC), which is different to the levelized cost of electricity. For non-thermal renewables and nuclear, SRMC is very low as there are no or very little operational costs. For fuel-consuming plants, like coal and gas, SRMC is more dependent on the fuel costs. Nonetheless, it is impossible to obtain the true short-run marginal supply curve as the data are commercially sensitive.
To simulate the system, we developed a bespoke short-run marginal supply curve for generation capacity representing 893 power plants, with a cumulative nameplate capacity of 86,880 MW based on the Digest of UK Energy Statistics36. We used SRMC (Supplementary Table 5) from the National Grid Electricity Scenario Illustrator (ELSI) model, which is an integrated power market economic dispatch model41. SRMC were assigned to each unit based on central operational cost estimates for 35 technology types42. However, for the simulation in this study, a plant-by-plant ordered supply curve is necessary for the partial equilibrium calculation of the strike price. Thus, cost variation was added to each individual unit depending on the age (see Supplementary Note 1), such that newer (and more efficient) units would have marginally lower operational costs than older plants.
Wind and solar have the lowest short-run costs (once installed, operation costs are basically zero) yet their output (capacity factor) is never actually equivalent to the nameplate capacity due to the variable wind and solar radiation conditions. Thus, the unadjusted supply curve is adjusted to represent low, medium and high estimate levels of combined wind and solar generation, in a method similarly used in ELSI and the UK Government’s Dynamic Dispatch Model43. Using daily production values from the years 2013 to 201644, 10th, 50th and 90th percentile daily production values for wind and solar were calculated (Supplementary Fig. 6), for each month, yielding three adjusted supply curves per month, 36 in total (Supplementary Fig. 7). For the rest of the generation capacity from other sources, capacity availability is assumed to be 100%, except for when thermal capacity is impacted by low flows as described above. This enables us to the test the sensitivity of low to high renewables production scenarios, whilst keeping the meteorological impacts more strictly focused on the electricity production impacted by low flows. Other studies investigating the variability of renewables explore this issue more comprehensively45,46. We also assessed the sensitivity to fuel prices, adjusted ±25% for coal, gas, biomass and oil (Supplementary Table 5, Supplementary Fig. 8).
Electricity demand model
We estimate a statistical model of daily electricity demand and strike price, including weather variables as co-variates. There is ample empirical data for electricity demand and price, so we use a machine-learning gradient boosting regression trees algorithm47,48 with the Huber loss function49, chosen for its ability to handle mixed datatypes and robustness to outliers when compared with squared error loss. The input variables for training the model were minimum, mean and maximum air temperature, mean wind speed, mean windchill, month, week number and day type (weekday or weekend). Windchill was calculated using temperature and wind speed inputs50. For observed climate variables, we used the UK Met Office MIDAS dataset51 for 2012–2017 inclusive, to derive a single GB climate timeseries, by population-weighting52 weather station data from 13 urban-area weather stations corresponding to the 13 most populous urban areas in Great Britain (Supplementary Table 2). The effect of this is significant with adjustment of −3 to +4 °C for the temperature timeseries compared with the unweighted average (Supplementary Fig. 2). Public holidays were also removed to improve model fit.
For input daily electricity demand, we re-sampled 5-min electricity production and demand data from Elexon/Sheffield University and processed by Gridwatch44. We used the k-folds (k = 10) cross-validation method53 to validate the model performance against unseen independent data (Supplementary Fig. 3). The model is trained and tested multiple times on k subsamples of the data, achieving r2 coefficient of 0.81, cross-validation score of 0.87 and percentage bias in overall electricity demand of −0.08%. Performance of the model was assessed in further ways to determine suitable representation of key features. These include fit of the load duration curve (LDC) (Fig. 8), representing seasonal, monthly and weekly profiles (Fig. 9, Supplementary Fig. 4), in addition to the statistical measures used in the cross-validation (Supplementary Fig. 3) and the methods. The LDC fits the observed period well, closely tracking the median LDC for the period (Fig. 8a). In addition, the climate uncertainty in grey lines all fall within the expanded observed uncertainty range (pink), which includes not only weather variability but also considerable socioeconomic factors. Slightly warming temperatures under climate change, not including socioeconomic changes and responses, we can see a slight flattening of the LDC with slightly less electricity used in wintertime (Fig. 8b). Percentage values of deviation are small across the distribution (Supplementary Table 3,, Supplementary Fig. 4). In timeseries format, the model output regular and cyclical, representing the key seasonal behaviour, as well as the weekly profile with lower demands at weekends (Fig. 9c).
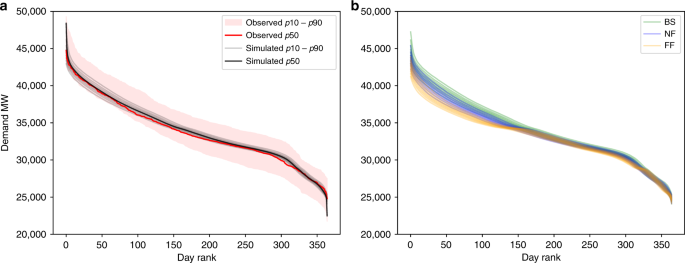
a Comparison of the observed LDC for 2012–2017 in red, with 100 simulated LDCs from the 100 W@H climate samples. Note that the observed uncertainty range is considerably larger due to other socioeconomic factors such as changing demand. b Comparison of the baseline, near future and far future LDCs using nine percentiles across the climate uncertainty.
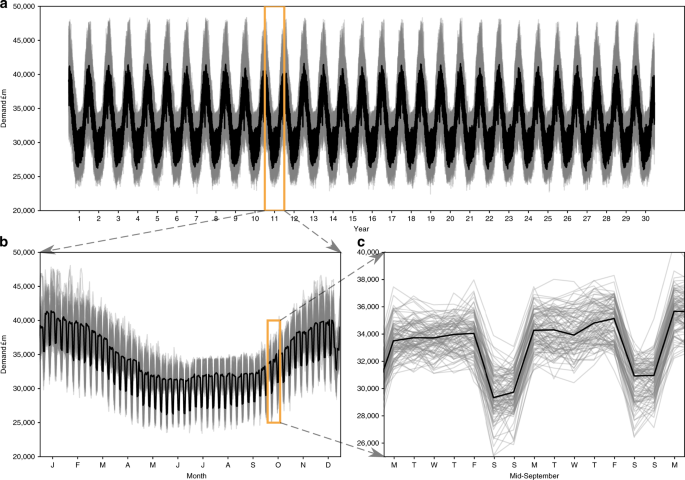
a The full 30-year timeseries. Lower panels zoom into the timeseries. b One-year profile for year 10, months January through December. c Two-week profile for year 10 in mid-September, Monday through Monday.
To generate daily electricity demand for the simulations, the daily gridded climate output data from W@H2 was population weighted using data from as inputs for the model (Supplementary Table 2).
Simulating price impacts
The merit order supply curve is typically determined by individual producers bidding (committing units) to provide a certain level of power at a designated time period and for a minimum price. Initial market supply price (strike price) is calculated at the intersection of demand with the supply curve. All plants that have bid below this supply price on the curve are now contracted to supply and will be paid the full strike price per unit of electricity supplied. This arrangement minimizes costs to the consumer whilst paying all suppliers the same commodity price.
When capacity is unavailable due to the low flows, the model removes this capacity from the supply curve on a daily basis. Depending on which plants are impacted and their position on the merit order, this shifts various parts of the curve to the left, resulting in a higher strike price to meet the same demand, as more expensive capacity has filled the gap. The new strike price is now paid to all suppliers up to that demand. In normal markets, changing prices would result in slight adjustments to demand, due to price–demand elasticities. However, this is not the case in the short term for wholesale electricity markets, because consumers are buffered by the retail market, for which the prices are only adjusted on much longer timescales, e.g. every few months or even annually when customers renew their contracts.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Source: Resources - nature.com



