Occurrence and trait data aggregation
Body size data for PEMA were obtained from three primary sources. First, we used digitized natural history specimen records aggregated in VertNet (vertnet.org52). We obtained standard total body length and mass measurements previously unlocked from the VertNet corpus using the approach of Guralnick et al.14. We then modified this approach, and developed new parser scripts to obtain additional, detailed body length measurements from specimen records, especially tail-length in this case, applicable for all non-volant mammals (see https://github.com/rafelafrance/traiter). Second, we collected the same body size data from the North America Census of Small Mammals (NACSM15,16,17,18,19,20,21,22,23). NACSM was part of the Rodent Ecology Project at Johns Hopkins University that coordinated small mammal censuses across North America15. While most surveyors associated with the study collected measurements from voucher specimens, our data extraction suggests that others were collected from live individuals, thus making this data source a mixture of the two types of measurements. We consulted annual NACSM reports and manually digitized a portion of PEMA records that contained associated head-body length and/or mass measurements. Third, we gathered body size data from the live mammal census records generated by the National Ecological Observatory Network (NEON; https://www.neonscience.org/)53. NEON data were extracted using the “neonUtilities” R package54. We aggregated all PEMA records that contained body length and/or mass measurements from these sources and harmonized data fields across sources for analysis.
We assembled datasets for two body size traits: body mass and head-body length. For body mass, we used known adult body mass ranges along with juvenile reporting (in VertNet records) to filter out records below 9 grams and reported juveniles, which represent unambiguous juvenile individuals55. We derived head-body length (HB Length) by subtracting tail lengths from overall total length13. Isolating HB Length is critical because tail length varies substantially in PEMA (and across Peromyscus), possibly as an anatomical feature used in locomotion and balance. All measurements were carefully hand-checked to flag obvious outliers, and records with trait measures more than 3 standard deviations from the mean for any measurement (i.e. body mass, tail length, or total length) were also discarded.
Finally, to fill spatial sampling gaps, we manually georeferenced some additional VertNet specimen records for which body size measurements were available. Our georeferencing protocols followed Chapman and Wieczorek56 and employed a combination of tools including Google Maps (https://www.google.com/maps) and the MaNIS georeferencing calculator57 (http://manisnet.org/gci2.html). Next, we manually georeferenced locations of NACSM census sites and paired the localities with body size data from that resource13. We also used verbatim geospatial data associated with NEON census sites for body size data from that resource.
Processing of specimen trait records for model construction
A final set of preparation steps were needed to create a model-ready dataset. First, we filtered remaining records that could not be georeferenced, that lacked date of collection or otherwise had unusable dates. We also removed those records without day or month reporting, and we removed records with collection dates of “1 January”, since these often represent misreporting of records where only year is known. We removed records that lacked sex reporting as well as those with ambiguous sex assignments such as “undetermined” or “female?”. The vast majority of those filtered records were VertNet records. We then derived two new fields: “season collected” and “decade”. We used month and day of collection to assign records to season categories (e.g. Spring, Summer, Fall, Winter defined by equinox and solstice dates) and we used decade of collection to bin records into decades. We only included records from 1895 onwards and binned into ten year increments. This created 13 decade bins, although the last was from only 2015–2019. For temporal analyses, we further filtered records as described below. Finally, to account for the possible effects of age class and spatially variable population demographic processes, we created alternate versions of our dataset with all juveniles labeled as such in the Darwin Core field “lifeStage” filtered from the analyses. This “no juvenile” dataset was used in analyses below. We also provide supplementary analyses with marked juveniles not excluded, since this increases sample size for analyses, and we do not expect biases in juvenile number over time or space based on collecting methods.
Pairing climate and population density information with records
Following aggregation from all data sources, we obtained paired historical climate data for georeferenced body size records using ClimateNA v6.058. ClimateNA is a reference tool consisting of past and present climate grids for mainland North America interpolated from long-term weather stations using the method of Mitchell and Jones59. We used geocoordinates of all body size occurrences as input into ClimateNA and augmented these with verbatim elevation values for records whenever available; the latter values are used for refining climate estimates within grid cells58. Default settings were used for all ClimateNA extractions. We extracted all climate variables for each body size record and later parsed mean annual temperature (MAT) and mean annual precipitation (MAP) of the year of collection for use in statistical analysis. Given the short gestation time (22–30 days) and average life-span (less than one year in the wild), using current year of collection for temperature and precipitation values is warranted.
We assigned human population density estimates to each record using human population density data for the USA from Fang and Jawitz60, who provided decadal human population density from 1790 to 2010. This high spatial resolution (1 km by 1 km) modeled human population density dataset serves as a proxy of urbanization and human disturbance. It is also unique in providing temporal depth, which is critical for our use here. Beyond the key temporal resolution provided by this dataset, we prefer population density over impervious land coverage as a measure of urbanization for two reasons. Urbanization is mainly driven by population and is a proxy for many other biotic and abiotic changes. As well, population density ranges from over multiple orders of magnitude while impervious land coverage has an upper limit of 1. Therefore, population density may quantify urbanization and disturbance more effectively. We note that because such data over time is only available in the USA, this step excludes records of PEMA from Canada and Mexico. Our analysis therefore is constrained to the conterminous USA. In order to assign a human population density record to each record, we used an R61 script that indexed the decade collected and spatial location of the specimen record to the correct human population density pixel in a stack of layers. We also assembled an estimate of human population density for each specimen record at 1 km, 4 km, and 10 km via pixel aggregation. All values for human population density were logged before use in models given that values can range over orders of magnitude.
Relationship between head-body length and body mass
We determined the relationship between head-body length and body mass using a simple univariate linear regression where log(HB Length) predicts log(body mass). We performed this analysis and examined variance explained before treating these two variables separately in analyses, since very strong fits would imply co-linearity. More detailed analyses using sex or season covariates are likely to be informative regarding the details of these allometric patterns, but were not done here, because the key prediction we are testing is that the relationship between the two key variables used in the rest of the analyses are relatively weak.
Defining spatial regions and replicates
We binned body size records into ecoregional categories to account for broad climatic variation across the range of PEMA and associated ecological differences among populations. We developed two binning approaches, used for separate spatial and temporal analyses described below. First, we used Level I ecoregions as defined by the United States Environmental Protection Agency (https://www.epa.gov/eco-research/ecoregions) but divided several ecoregions more finely given the major climate and latitudinal range that some ecoregions encompass. Specifically, we split 3 of the Level 1 ecoregions (‘Great Plains’, ‘Northwestern Forested Mountains’, and ‘North American Deserts’) at 42 degrees latitude and re-designated the resulting ecoregions (‘Northern and Southern Great Plains’, ‘Northern and Southern Cordilleras’, and ‘Northern and Southern Desserts’, respectively; Fig. S1). We then extracted ecoregional membership for PEMA occurrences using the over function in sp62 in R.
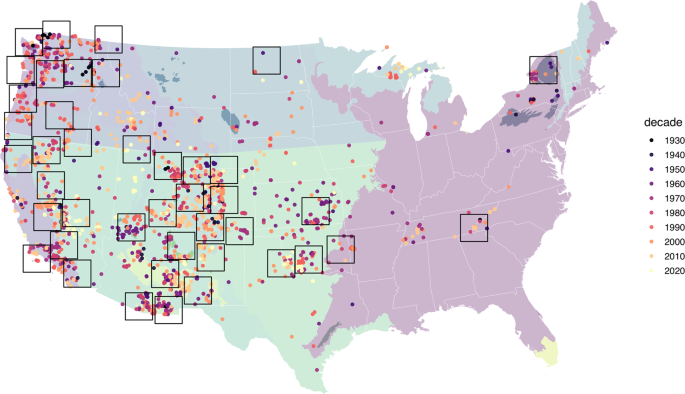
In order to aggregate PEMA body size records into spatiotemporal replicates at sub-ecoregional scales, we developed a second spatial binning approach employing 200 × 200 km grid cells. The goal of the binning approach was to identify those areas where sampling has been most dense over time, and to use these spatial areas in random effect models as replicates to understand different dynamics of change in temperature, and human population density. To optimize the number of spatial replicates, we developed an R script that sampled individual grid cells at random across the contiguous U.S. and retained cells if they met the following criteria: 1) At least 75 total records; 2) At least 4 decades represented and; 3) At least 10 records per decade. To optimize the sample sizes within grid cells, we resampled cells at random for up to 200,000 iterations, replacing existing cells with new cells if they were overlapping and contained higher total numbers of body size records. Figure 1 shows an example zonation using all data records.
Because the number of records per decade was part of our optimization criteria, we filtered our original full dataset to create temporal datasets that only included records collected since 1945. While this filters records collected in the early part of the 20th century, those records are much sparser than records during the second half, especially given the inclusion of NACSM data that begins in 1948 and provides strong spatial coverage. We show just how sparse data are in Fig. 2 that documents trends in number of records separately for each data source we used.
We provide a summary (Tables 1, S1, S2, Supplementary Results) of the 12 final datasets, covering 2 different key body size traits, with and without labelled juveniles, with and without NEON as a source, and across spatial and temporal filtering, that were used in this analysis. That supplementary material provides information on the total number of records included, and number of zones, for the spatial and temporal datasets.
Spatial and temporal analyses of body size drivers
Spatial analyses
Our first models examine only spatial predictors of PEMA body size and therefore assess Bergmann’s Rule as it is typically conceptualized. We focus separately here and below on body mass and HB Length as response variables. As a multitude of factors may influence changes in PEMA body size, we ran a suite of linear mixed-effects models, using the R package lme463, in order to identify what factors influence spatial variation in body mass and HB Length. We ran a series of 29 candidate models, with the global model consisting of five fixed effects: Mean Annual Precipitation (MAP), Mean Annual Temperature (MAT), sex, season collected (coded as Spring, Summer, Fall and Winter), and human population density. We also included two random intercepts, ecoregion and data source (VertNet, NACSM, NEON). The data source covariate is used to assure that there is not a systematic bias in how measurements were taken across the different data resources we assembled. We did this because measurements from live-trapped individuals can be less precise and harder to obtain than from euthanized voucher specimens (e.g.49). In all cases, we mean-centered and standardized continuous predictors, and transformed categorical predictors to factors. In addition, we checked model residuals and found no evidence of spatial autocorrelation. In reporting model results, we provide summary statistics needed for interpretation, including model p-values, but emphasize those less compared to model support values. Based on our results, all HB Length models of spatial variation were run a second time but removing NEON data. We also determined the marginal and conditions R2s for the best models as determined via model selection.
Analyses with decadal covariates
To assess temporal body size trends, we ran a series of 44 candidate models with six fixed factors in the global model, including MAP, MAT, sex, decade, season, and population density. In these models, we also included a random slope of decade nested within zone. As before, these models were separately run for both body mass and HB Length. NEON data were excluded given bias in HB Length and to avoid unaccounted decade by source interactions given the different sampling approach. All sets of spatial and temporal models were run with and without juvenile PEMA. Models were fit using the R package lme4. Model fits were assessed and ranked with AICc using the R package MuMIn64. We examine model diagnostics as above and, in these analyses, particularly examined random effect results to determine correlations between slope and intercept of the random terms since this informs whether larger or smaller PEMA as stratified by zone show similar or different trends in body size change over time. For comparison with the random effects models, we also performed exploratory analyses where we fit body size by decade independently for each zone.
Source: Ecology - nature.com


