Density-dependence tips the change of plant–plant interactions under environmental stress

Model

A detailed model description is provided in the Supplementary methods. Here, we only illustrate the core equations. In the model, an individual’s potential growth rate (without neighbors) is defined as:

where m is total mass, a is a species-specific constant, and M is the theoretically maximum mass. S is the stress intensity quantified as the proportional reduction in incoming energy. It ranges from 0 (no stress) to 1 (extreme stress and no resources).

The equation is based on Metabolic Scaling Theory⁵² and it was integrated with the zone-of-influence (ZOI) model to include interactions⁵³. In the spatially-explicit ZOI model, each plant is modeled as a circle and its size (A, unit: area) denotes potentially available resources and is allometrically related to the biomass, as A = C₀m^3/4, where C₀ is a constant (see Supplementary methods). Individuals interact with each other where their ZOIs overlap. Therefore, the realized growth rate is as follows:

where r indicates the intrinsic growth rate (in mass area^–1 time^–1) while I_c and I_f are competition and facilitation indexes, respectively. I_c represents the proportion of actual resources available for an individual under competition:

where A_c represents the actual resources a plant can obtain. It is calculated as the sum of the nonoverlapping area and the effective that can be obtained within overlapping zones. The division of overlapping areas is determined by the parameter p, i.e., the mode of competition⁵³. It ranges from 0 (complete symmetry) to ∞ (complete asymmetry). In harsh conditions, the size of ZOI also reflects the quantity of perceived stress and stress mitigation occurs in overlapping areas. Similarly, I_f is the proportion of realized stress for an individual experiencing facilitation:

where A_f is a quantitative measure for stress reduction by neighbors. Likewise, the calculation is based on how individuals share overlapping ZOIs (stress), which is determined by the parameter q, i.e., the mode of facilitation⁵¹. It also ranges from 0 (complete symmetric facilitation) to ∞ (complete asymmetric facilitation). See also Supplementary methods for detailed calculation process about I_c and I_f.

Compared to previous models, a main improvement is the explicit consideration of the impact of the size of the beneficiary on its facilitative response. Previous studies have used the term S/(1 + A_f) for effects of stress and facilitation on plant performance^{31,40,49,50,51}. For a given stress level, this term is determined only by A_f, i.e., positive effects of benefactors. However, this term is not realistic because it cannot reflect differential sensitivity of beneficiaries with different size to stress amelioration (facilitative response, see Fig. 5 for example). Thus, the influence of facilitation was identical: S/(1 + A_fa) = S/(1 + A_fb), as long as stress alleviation by benefactors was the same (A_fa = A_fb), although the smaller plant should experience stronger facilitation. A fundamental problem arising from that approach is that the unit of A_f (area^–1) is not balanced in the term S/(1+ A_f), and units on both sides of the growth equation are not identical. Namely, the units are mass time^–1 on the left side but mass time^–1 area^–140,51 or even more complicated on the right side^31,50. Here, we included facilitative response via the term SI_f = S(1 − A_f/A), which is both more realistic and mathematically correct (equal units: mass time⁻¹).

Fig. 5: Schematic illustration of stress amelioration for plants with different size in a zone-of-influence (ZOI) model.

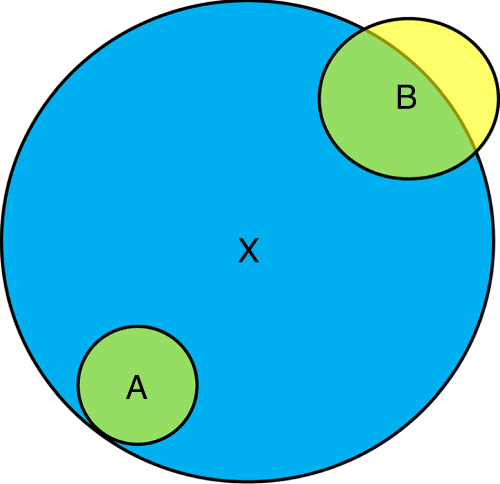
A and B (yellow ZOIs) are two conspecific beneficiary plants and they are facilitated by a benefactor X (blue ZOI). The stress intensity (e.g., salinity) per unit area is homogeneous across space. The area of overlap of ZOIs (green) is the same for both beneficiary plants (A_fa = A_fb). However, plant A fully benefits from the presence of X while B benefits only partly. Thus, beneficiary A will respond more positively to habitat amelioration than beneficiary B, i.e., the facilitative response is size dependent.

Full size image

The simulations were done in Netlogo (version 6.0.1)⁵⁴ using a grid of homogeneous patches (200 × 200) in a continuous two-dimensional space⁵³ with a wrap-around approach to avoid edge effects⁵⁵. Data were collected every ten time steps and results presented after 50 steps. Plants experienced a density gradient with seven levels from 2 to 8 (in scale), which also encompassed the density range of our experiment, Namely, in the control (without stress), the competition intensity at the minimum and maximum density level in simulations should be lower and higher than that in the experiment, respectively. Following previous studies^22,31, density refers to initial density and not surviving density. We explored a wide range of stress levels and for ease of visualization, present here four of them: no (0), low (0.45), high (0.75), and extreme (0.85), respectively. Other stress levels yielded the same qualitative results (Supplementary Fig. 1). We also evaluated potential effects of spatial distribution (random, regular, aggregated) and different modes of competition and facilitation, but these did not change the qualitative findings either (Supplementary Fig. 5). In the following, we thus mainly present results for the scenario most similar to the intraspecific experiment, i.e., random distribution, symmetric competition (p = 1) and symmetric facilitation (q = 1). Each simulation was repeated five times. Considering that plant–plant interactions may change over time due to individual growth, we also ran additional simulations. Thus, in each time step, we collected data of the mean biomass under relatively high stress where strong facilitation occurred, i.e., S = 0.75 and 0.85.

The RII was used to quantify strength and direction of net plant–plant interactions⁵⁶:

where P_W and P_S are the performance of plants with and without neighbors, respectively. RII ranges from −1 to 1 with negative values indicating competition and positive values net facilitative interactions. To estimate biomass of individuals without neighbors (P_S), we calculated the growth rate as follows:

Experiment

The experiment was set up in a greenhouse at Tübingen University between early October and mid December 2015 (light intensities: 130–150 µmol m⁻² s⁻¹ and 16 h day⁻¹; temperatures: 15 °C (night) and 20 °C (day)). We selected the model plant Arabidopsis thaliana as study species because it is annual and fast-growing, densities can be easily manipulated, and standardized seed material enables to conduct experiments with essentially similar plants. Moreover, previous research has revealed strong intraspecific facilitation under salt stress for this species³⁴ such that the general system was well established. Seeds of A. thaliana (popular Columbia wildtypes) were obtained from Nottingham Arabidopsis Stock Centre and inbred lines raised for one generation to amplify seed numbers.

Seeds were sterilized in 70% ethanol for 2 min and stratified at 4 °C for 5 days⁵⁷. They were then transferred to pots (10 × 10 × 10 cm) with standard potting soil (Einheitserde Classic, Gebr. Patzer Company). Seeds were sown to obtain a density gradient, i.e., 1 (without interactions), 2, 3, 5, 7, 10, 15, 20 seedlings per pot, respectively. Considering the small pots, 20 individuals per pot was actually very dense (i.e., 2000 plants per square meter). Approximately twice the number was sown in each pot for making sure that the desired seedling numbers can be obtained even under incomplete germination. We further prepared 40 additional pots with 10 seeds each as backup. Three days after germination, randomly selected surplus plants were removed. 60 spare individuals were transplanted to pots with insufficient germination. Plants growing with fewer neighbors may suffer more from stress⁵⁸, and we observed high mortality of single plants under high salinity in our pilot study. We therefore set more replicates for low densities to obtain enough individuals for the analyses, i.e., 50 for density 1, 30 for 2 and 3, and 20 for each of the higher densities, respectively.

We applied the following four treatments: 0 (no salt), 50 (low), 100 (high), and 150 mM NaCl (extreme) solution. They were selected based on a previous study³⁴ and they were meant to capture the entire possible range from no stress to extreme stress i.e., 80% limitation in performance such as growth and/or survival for plants without neighbors³⁵. Naturally observed stress levels in saline habitats are well within this range, e.g., highly saline conditions may limit growth by up to about 70–75%^29,43. Salt was first applied eight days after germination and plants were watered every 5–7 days depending on soil water conditions. Each pot received the same amount of liquid at each irrigation event, and the amount was successively increased from 50 ml to 150 ml as plants grew. The location of pots assigned to different treatments was fully randomized. At the end of the experiment, we counted the number of survivors in each pot and determined the number of siliques and above-ground biomass (dried at 70 °C for 24 h) per survivor.

RIIs were also calculated according to Eq. (5). Since the experiment was an intraspecific setting, we calculated P_W and P_S as the mean individual performance per pot without and with interactions, respectively³¹.

Statistical analysis

We applied Bayesian inference and fitted different models to the dataset of RIIs of simulations and the experiment, respectively (sample size in each treatment were provided in Source data). To compare our own conceptual model with existing theory, four models (Table 1) were fitted: (1) only stress as explanatory variable, which corresponds to classical facilitation models, i.e., SGH, a unidirectional change of RII along a stress gradient; (2) only density, i.e., classical competition models; (3) both density and stress (without the interaction term), i.e., the model that the RII–density relationship simply moves upward with increasing stress); (4) density, stress and their interactions (our own model).

When calculating the joint posterior distribution and uncertainty intervals of each model parameter, we selected uninformative Gaussian priors because there were few previous studies considering how density-dependence of facilitation could change along stress gradients⁵⁹. In the calculation, Markov chain Monte Carlo (MCMC) were applied with 20,000 iterations⁶⁰. After the estimation of posterior, we further investigated the convergence, i.e., whether MCMC chains converged to the posterior ((hat R , < , 1.05)). The Watanabe–Akaike information criterion (WAIC) was used for comparing these Bayesian models and the model with the smallest WAIC value was selected to be the best model⁶¹. The uncertainty in model selection was also evaluated, by using weighted averages of all the models^59,62. All Bayesian statistics and data calculations were performed in R (version 3.6.1)⁶³ using the package brms⁶⁰, which is based on the probabilistic programming language Stan⁶⁴.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Source: Ecology - nature.com