Evolutionary history and past climate change shape the distribution of genetic diversity in terrestrial mammals

Georeferencing and aligning sequence data

We obtained mitochondrial sequence data for terrestrial mammals from GeneBank and BOLD. GenBank data were downloaded on 16 May 2017 using the Entrez Utilities Unix Command Line. Data from BOLD were downloaded on 25 May 2017 directly from BOLD webpage using the application-platform interface (API) (http://www.boldsystems.org/index.php/resources/api). Our mammalian database consisted of 110,218 sequences for cytochrome b (cytb) and 43,961 sequences for cytochrome oxidase 1 (co1).

We assigned geographic coordinates to the sequences that were not already annotated with latitude and longitude using the API tool provided by GeoNames.org (http://api.geonames.org). To increase the quality of the data in our georeferenced database, we excluded from this procedure any sequences that had only the country name as locality information. From the full set of georeferenced sequences, we extracted all base pairs corresponding exclusively to cytb or co1 by mapping the sequences against the reference mitochondrial genome of Lepus europaeus (accession number: AJ421471). Sequence mapping was performed in Geneious v8.1.7 (ref. ⁵⁶) using default settings. We then extracted all base pairs that were successfully mapped against the homologous cytb and co1 loci of the reference genome. For each unsuccessfully mapped sequence we extracted all cytb and co1 base pairs using customized Shell scripts¹¹. After the mapping, we further removed all sequences with IUPAC ambiguity codes. Following these filtering steps, species-specific alignments were generated using default settings in MUSCLE⁵⁷. The enriched georeferenced and aligned dataset included a total of 54,786 mitochondrial sequences for 2128 species (1690 species for cytb, 1153 species for co1), representing overall, 36% of the available cytb and co1 sequences at the time of retrieval.

Filtering out georeferenced sequences

As we were only interested in the natural range of extant species, we spatially filtered out sequences outside the known native ranges of species. We first checked the spatial concordance between the georeferenced sequences and species’ geographic ranges obtained from the most recent version of IUCN geographical ranges (v6.2) for terrestrial mammals⁵⁸. We used the IUCN species range polygons (ESRI-formatted shapefile) and excluded polygons with presence values of 3 (“possibly extant”) and 6 (“presence uncertain”), as these represent highly uncertain estimates of distribution. We also excluded range polygons with origin values of 3 (“introduced”) and 4 (“vagrant”). We then compiled a comprehensive database relating the IUCN accepted species names with all available species synonyms for terrestrial mammals. We obtained species synonyms from a previous study⁵⁹ and the Integrated Taxonomic Information System (https://www.itis.gov/). For cases where we found no match between IUCN and the sequence databases, we further checked the relevant literature and identified synonyms. In some cases, two or more species from GenBank were matched to one single species in IUCN. These cases mostly reflect recent taxonomic revisions and newly described species not yet assessed by IUCN. For the spatial filtering in these cases, species were treated as one single species, following the taxonomic nomenclature of IUCN, and sequences falling outside the ranges of IUCN accepted species were excluded.

For each sequence, we calculated the minimum distance between the boarders of the respective range polygons and the sequence coordinates, and excluded sequences with a minimum distance >385.9451 km (the selected resolution of the grid cells; see below). The final filtered sequence database included 24,395 sequences for cytb and 22,570 sequences for co1 (Supplementary Figs. 1–3).

Calculating GD

We defined GD as nucleotide diversity—that is, the average number of nucleotide differences per site in a pairwise sequence comparison¹¹. GD within species was then defined as the average number of nucleotide differences per site across all pairwise sequence comparisons for that species. It is mathematically defined as

where k_ij is the number of different nucleotides between sequence i and sequence j, ((frac{n}{2})) represents the number of pairwise comparisons made, and m_ij is the number of shared base pairs between sequence i and j. We considered only pairwise comparisons where sequences overlap in at least 50% of the longer sequence and ignored all positions with gaps or “N” (unknown nucleotide). For a particular assemblage of species, GD was calculated by averaging nucleotide diversity per site across all species present in that assemblage. Thus, we calculate the GD of the assemblage t (GD_t) with genetic sequences from S species as

We calculated GD at two spatial grain resolutions and for both markers independently:

(1) Equal-area grid cells. To map the distribution of GD at a finer scale across the planet, we defined an equal-area grid (Behrmann cylindrical equal-area projection) with cell size of 385.9 km × 385.9 km representing 148,953 km² area grids. This grid cell area has been previously shown to be the most appropriate for maximizing the number of sequences from each species that are included in the calculations of Π (Eq. 2) and minimizing the difference in the number of sequences between species¹¹. We then assigned each georeferenced sequence to a grid cell and calculated GD of each cell as described above.

(2) Wallace’s zoogeographic regions. To compare GD across independent evolutionary regions of the planet for terrestrial mammalian species and account for phylogenetic relationships across species, we calculated GD across the updated Wallace zoogeographic regions⁴¹ (34 regions, Supplementary Fig. 3). GD for each region was calculated as described above.

SR and PD

We evaluated the global spatial correlation between GD at intraspecific levels and the two main biodiversity dimensions at the interspecific level—that is, SR and PD. To this end, we first identified species ranges intersecting each spatial unit (that is, grid cells and zoogeographic regions) using the IUCN species ranges described above⁵⁸. We then calculated SR as the total number of species in a given spatial unit. To be consistent with the estimates of PD (see below), we estimated SR as the total number of species in a given spatial unit that were also present in the mammalian phylogeny. To estimate PD, we obtained a dated mammalian phylogeny from a recent study⁵⁹. While this phylogeny is the most comprehensive dated phylogeny for mammals to date, we acknowledge that branch length information may be inaccurate, particularly for branches that have not been dated previously⁵⁹. However, this reduction in accuracy is likely to be fairly small and restricted only to a portion of the external branches⁵⁹, thus expected to have minor impact in our global estimates of PD (see also ref. ⁴). We first calculated PD as the sum of tree branches (branch length is measured in millions of years) connecting all species occurring in each spatial unit⁶⁰ for all 1000 trees from the posterior distribution of the published phylogeny. We then estimated PD per spatial unit as the mean PD across all 1000 trees.

Climate stability

We calculated climate stability for temperature and precipitation during the most recent inter-glacial period by calculating centennial trends and variability around the trend. We did this because these two measures of stability capture complementary information on low frequency/long-term (that is, centennial trend) and high frequency/short-term (standard deviation [SD]) climate variation^42,43. Based on theory, we expect that regions with long-term stable climate (low trend in temperature and precipitation) and short-term unstable precipitation (high SD), during periods of rapid change in global mean temperature over the past ~ 21,000 years, will coincide with locations that have experienced less population extinction and population adaptive divergence, thus high GD. Paleoclimate data from the TraCE-21ka experiment were extracted using PaleoView⁶¹ at a monthly time-step between 21,000 bp and industrialization (1850 ad; 100 bp). We first identified past centuries of rapid change in global annual mean temperature (that is, extreme centuries) as those having global mean temperature trends (that is, slopes of the generalized least-squares regression) greater than the 90th percentile of the cumulative distribution function built from the trends within all past centuries (1-year time step between windows)⁴³. We then calculated local measures of century time-scale trends for each grid cell (n = 10,368 cells, 2.5° × 2.5°) for the identified extreme centuries in global mean annual temperature⁴². We also calculated grid cell estimates of variability, where variability was defined as the standard deviation of the residuals about the local trend⁴³. We calculated the median trend and median variability across time (that is, across all extreme centuries of change in global temperature) for both temperature and precipitation. We then extracted the values of the climate grid cells intersecting each spatial unit/polygon (grid cells, zoogeographic regions) and calculated the mean value of each climate variable within each spatial unit.

Human footprint

We tested the effects of both historical and recent human land modification on the global distribution of GD. To estimate historical land modification, we used the KK10 anthropogenic land cover change dataset⁶² that provides grid cell-based estimates of anthropogenic land-cover change (ALCC). The KK10 dataset quantifies anthropogenic impacts on terrestrial carbon storage by combining a global vegetation model with an empirical relationship between population and land-use based on observed data from a number of European countries over preindustrial time⁶². The model output is used to evaluate the impacts of humans on land-use and its subsequent effects on terrestrial carbon storage during the preindustrial Holocene. The data cover the period from 8000 bp to 100 bp, at a resolution of 0.08° × 0.08°. The model assumes that the physical environment over time is stable (that is, climate or geomorphic change was stable over the Holocene). Despite this major assumption, independent validation (for Northwestern Europe), using information on vegetation communities from pollen cores, has shown that the model performs well when predicting land-use change through the Holocene at a coarse country-level resolution⁶³. To evaluate the impact of ALCC during the Holocene prior to industrialization, we identified the time when each land cell is simulated to have surpassed a 20% threshold of human induced land-cover change. The 20% exceedance threshold for significant impacts has been used before for assessing historic human land-use impacts on the biosphere⁴⁵. For cells that were not simulated to be impacted by human land-use prior to industrialization (e.g. Greenland, Antarctica, some parts of northern Canada), a value of 0 was assigned.

For a more recent (post industrialization) estimate of human-driven land-use change, we used a remotely sensed estimate of the human footprint on the terrestrial environment (∼1 km² resolution at the equator) corresponding to the year 2009 (ref. ⁴⁶). This variable integrates remotely sensed and bottom-up survey information on the following human pressures: (1) the extent of built environments; (2) crop land; (3) pasture land; (4) human population density; (5) night-time lights; (6) railways; (7) roads; and (8) navigable waterways. These pressures are weighted according to estimates of their relative levels of human pressure⁴⁶ and summed together to create a standardized human footprint for all non-Antarctic land areas (values range from 0/no pressure, to 50/maximum pressure).

Linear regressions and effect of data availability

We first evaluated the distribution of GD at the grid cell and zoogeographic regions scales. As the distribution of GD at the grid cell scale was highly skewed towards zero, we transformed GD to normality using its square root. All subsequent statistical analysis at the grid cell scale were based on the transformed GD. We kept all eight independent variables in their original units. We then explored the association between the global spatial pattern of GD and the eight independent variables—that is, SR, PD, trend and variability in temperature, trend and variability in precipitation, and historical and recent human footprint—using simple linear regressions across genetic markers (cytb, co1) and spatial scales (grid cells, zoogeographic regions). Initial analysis at the grid cell scale revealed striking differences in the taxonomic coverage and sequence availability across cells (Supplementary Figs. 1 and 2). Taxonomic coverage is defined as the ratio between the number of species used for estimating GD and the total number of species naturally occurring in each grid cell estimated from IUCN range maps. These differences in data availability are expected to impose biases in our spatial estimates of GD due to limited information in the majority of grid cells. To overcome this limitation, we contacted all statistical analyses using multiple subsets of our full dataset (that is, all cells with GD information) based on two filtering criteria—that is, the minimum taxonomic coverage and a minimum number of sequences per grid cell. We fixed the minimum number of sequences per grid cell to one standard deviation of the distribution of the total number of sequences per grid cell in the full dataset (standard deviation for cytb = 55; standard deviation for co1 = 268). By keeping the data-rich grid cells (high taxonomic coverage or a minimum number of sequences) we were able to reveal the high correlation between GD and SR and PD, as well as the effects of climate stability, in explaining spatial patterns of GD at the finest scale and across both genetic markers (Figs. 1 and  2). The results of the linear regressions across the two scales and genes are given in Supplementary Figs. 4 and 5. We further provide all pairwise correlations among the eight explanatory variables in Supplementary Tables 1 and 2.

Since all the diversity variables show some spatial structure (that is, higher values towards the tropics), and all these variables are measured over the same locations, we further tested the significance of the association between GD and PD and SR using the modified t-test of spatial association⁶⁴ as implemented in the SpatialPack R package⁶⁵. We tested the spatial association across all the subsets of our full dataset described above (see also Fig. 2) and the results are given in Supplementary Tables 3 and 4.

Hierarchical partitioning

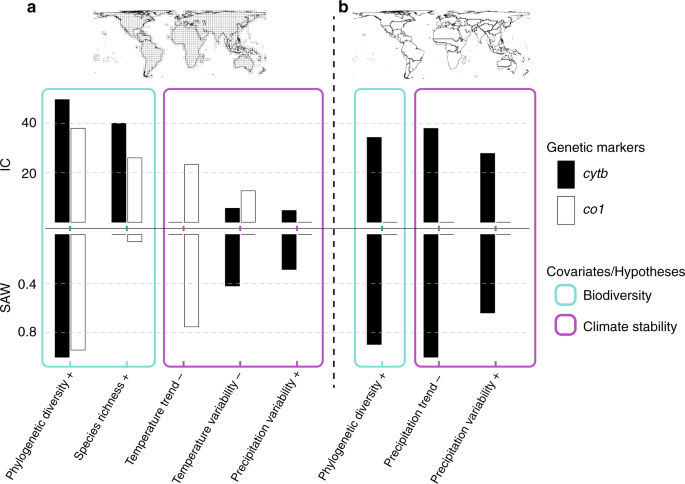
We used a hierarchical partitioning approach⁶⁶ as implemented in the hier.part R package⁶⁷ to test for the significance of the independent contribution of the eight variables on the global spatial pattern of GD. This approach allows the estimation of the independent contribution (IC) of each predictor variable in the total explained variance by considering all possible combinations of explanatory variables using linear regressions⁶⁶. The calculation of IC is based on the improvement of model fit (that is, increased R²) by incrementally adding variables starting from a simple single-parameter regression for a given variable and then averaging the model fit differences over all combinations in which that variable occurs. This approach has advantages over alternative techniques as it allows for the joint evaluation of multiple independent variables in the presence of multicollinearity^66,68 (e.g. between SR and PD). We estimated the significance of IC by randomizing the values of each explanatory variable 1000 times to obtain 1000 simulated values of IC. We then estimated the significance of each variable’s IC using the 95th percentile values of the simulated IC values and the observed IC value of each variable⁶⁷. To remove the effects of non-significant variables in our final estimates, we applied the hierarchical partitioning approach in an iterative fashion, whereby we started by including all eight variables and at each iteration we excluded the variable that showed the lowest (and insignificant) contribution. Iterations stopped when all retained variables were significant. Results of the hierarchical partition across the two genetic markers and the two spatial scales are given in Fig. 1 and in Supplementary Table 5. Note that all independent variables for co1 at the zoogeographic scale were insignificant. Also note that for the grid cell scale we only present results obtained using the data subsets containing data-rich cells both for cytb and co1 (see “Linear regressions and effect of data availability” section).

Multimodel inference and predicted GD

To identify the models that best explain the global distribution of GD in terrestrial mammals across genes and spatial scales, and further check for consistency with the IC values obtained from hierarchical partitioning, we applied multimodel inference using the corrected Akaike’s information criterion⁶⁹ (AICc). To this end, we first fitted linear models for all possible combinations of significant variables retained after the hierarchical partition step and excluded models that contained highly collinear variables (Pearson’s |r| > 0.7)^70,71. Applying this threshold removed the effects of redundant models that included variables within the same explanatory hypothesis (e.g. SR and PD, or temperature variability and temperature trend). Collinearity among variables representing different hypotheses was observed only for co1 at the grid cell scale (see Supplementary Tables 1 and 2 for collinearity among independent variables). Subsequently, for each model we calculated the AICc, ranked the models according to their AICc, and calculated the difference (ΔAICc) between the AICc value of the top-ranking model and the AICc value for each of the other models. We then excluded models with ΔAICc > 5 as models with higher values are commonly considered uninformative^69,72 (varying this threshold to a maximum of 10 had minor effects on the model selection procedure; results not shown). We then recalculated the Akaike weight for each of the retained models. Finally, for each variable across the retained models we summed the Akaike weights for each model in which that variable appears⁶⁹. The SAW is a proxy for the relative importance of variables under consideration. The results of the multimodel inference across spatial scales are shown in Fig. 1, Tables 1 and 2, and Supplementary Table 6. Like the hierarchical partitioning analysis, we only show the results obtained using data with a minimum taxonomic coverage of 7% or a minimum number of sequences per grid cell for both genetic markers.

To further test the adequacy of linear models in explaining global patterns of GD, we visually inspected the normality in residuals using QQ plots (Supplementary Fig. 7) and tested for residual spatial autocorrelation for each retained explanatory model across spatial scales using Moran’s I and 10,000 simulations implemented in the python package PySal v.2 (https://pysal.org/). Spatial autocorrelation in residuals would be indicative of violation of the assumption of independently and identically distributed residuals and can increase type I error rates (that is, falsely rejecting the null hypothesis of no effect of the independent variables)⁷³. It further indicates failure to account for important spatial processes/variables that induce spatial structuring in the dependant variable⁷³. Spatial weights were defined using the simple contiguity criterion for the zoogeographic scale, and the k-nearest neighbour criterion with k = 4 for the grid cell scale. We detected no significant spatial autocorrelation in model residuals across spatial scales and genetic markers (Tables 1 and 2) and these results were robust regardless of the choice of k (one to four).

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Source: Ecology - nature.com