Multi-scale spatial genetic structure of the vector-borne pathogen ‘Candidatus Phytoplasma prunorum’ in orchards and in wild habitats

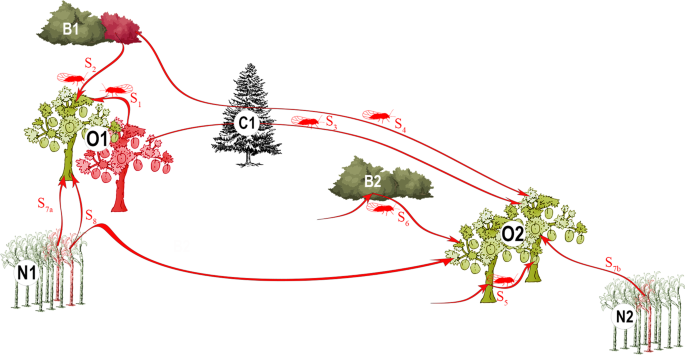
Study area and sampling

In each growing area, we mainly sampled (90%) apricot (Prunus armeniaca L.) orchards (Supplementary Table S1); the remaining 10% of sampled orchards consisted of cultivated myrobalan plum (Prunus cerasifera Ehrh.), European plum (Prunus domestica L.), Japanese plum (Prunus salicina Lindl.) and peach (Prunus persica (L.) Batsch) trees. Most of the samples were collected from symptomatic trees during the autumn and winter of 2010 and 2011 (Supplementary Table S1). We also included samples obtained in previous years (2007, 2008 and 2009). From each tree, we sampled 2–3 lignified shoots from different main branches. After molecular tests to assess the presence of the phytoplasma (see below), four to six plots were chosen in each region for a more comprehensive sampling (Supplementary Table S1). This was done from winter 2010 to early spring 2011. In this second sampling, all the symptomatic trees were sampled (thus, some trees were sampled several times for confirmation of previous molecular analyses; see below). To estimate the number of asymptomatic trees (data unknown at the beginning of the study but crucial to estimate the potential role of orchards as inoculum reservoirs), one out of every three trees was also sampled (i.e., systematic sampling). Between 78 and 244 trees per plot were analysed, depending on the size of the plots (Supplementary Table S1). A total of 2,656 samples collected in 69 different orchards were used in the study (Supplementary Table S1). In parallel, we sampled wild blackthorn (Prunus spinosa L.) or myrobalan bushes around the plots, at up to 30–40 km (Supplementary Figs. S2, S3 and S4). We collected between 5 and 46 branches in 61 bushes (21 branches per bush, on average), for a total of 1,114 samples (Table 1; Supplementary Table S1). We massively collected mature C. pruni adults using a beating tray (80 × 80 cm). Other congeneric species where sometimes caught but C. pruni individuals were easily recognized by the colour of the forewing, which is dark brown at the apex and brown in the remaining part. Soon after identification, we conserved the samples in 96% ethanol until DNA extraction. Phytoplasma-carrying insects collected several years before in the three regions were also included in the analysis (Supplementary Table S1). Thus, a total of 2,572 psyllids sampled from 71 different bushes were analysed (Table 1; Supplementary Table S1). We recorded the GPS coordinates of all collected samples, except for the systematically sampled orchards where we attributed a unique GPS coordinate — corresponding to the centre of each plot — to all the corresponding samples (Supplementary Figs. S2, S3 and S4).

Genetic analyses

The protocol used for the total DNA extraction from plant samples was adapted from Ahrens and Seemüller⁴⁷. Briefly, for each plant sample, the phloem was isolated by removing the outer bark with a knife and by scraping off the layer of vascular tissue with a scalpel. Fresh phloem tissue was then ground in individual bags (0.5 g per bag). All the Prunus samples were individually analysed. DNA from plant samples was then purified using the CTAB method⁴⁸ in 1.5-ml tubes. DNA pellets were diluted in 100 µl of pure water. Total DNA of individual psyllids was purified from whole bodies, and each psyllid DNA sample was assigned to species A or B by amplifying the Internal Transcribed Spacer 2 (ITS2), as previously described³⁷. No individual showed two bands, demonstrating that the sample was devoid of hybrids or contamination between species.

To select samples for sequencing, ‘Ca. P. prunorum’ was detected in the insect and plant samples by using the ESFYf/r primers in a specific and sensitive PCR-based method, as described in Yvon et al.⁴⁹. We then attempted to sequence the 1,328 positive samples at the immunodominant membrane protein (imp) gene locus, which was shown to be highly variable for ‘Ca. P. prunorum’³⁵ and assumed to be present at a single copy per genome based on the known genome sequence of ‘Ca. P. mali’⁵⁰, a closely related phytoplasma (i.e., belonging to the same taxonomic group, 16SrX). DNA amplification performed well for almost all of the psyllid samples, but failed for more than a quarter of the plant samples (Table 1), which we attributed to the presence of putative inhibitors like polyphenols⁵¹ in the unevenly infected woody material. Successfully amplified imp DNA was purified and Sanger-sequenced in both directions by Genewiz (Takeley, UK). Chromatograms were trimmed, assembled, and aligned using the Muscle algorithm, and visually checked under Geneious (version 5.5) (http://www.geneious.com). Sequences were deposited in GenBank (accession n° MN116709 to MN116718; Supplementary Table S6). SNPs between individual sequences were detected, and ‘Ca. P. prunorum’ genotypes were defined according to Danet et al.³⁵ When previously undescribed SNPs were detected, we performed a second independent extraction from the same sample, followed by amplification and sequencing to ascertain the new imp sequence. To represent genealogical relationships among sequences, we used POPART software⁵² (v.1.7) to build a genotype network using the integer neighbour-joining (IntNJ) algorithm, which is well adapted for low-divergence datasets. Each infected individual contained a single imp genotype, except for six cultivated trees in which two different genotypes were found (either from different branches or in different years) and kept for the analysis.

Statistical analysis

All statistical analyses were performed using R 3.4.0⁵³. A correspondence analysis was performed on the contingency table (Supplementary Table S3) using the coa function in the ade4 package⁵⁴, and we visualised the results with the factoextra package⁵⁵. The contingency table was also directly visualised using the table.value function in ade4 to uncover specific association patterns. To test whether the distribution of genotypes among compartments differed between the three regions, we carried out multinomial regressions with the nnet package, and we tested the interaction between compartments and regions by comparing (using a likelihood ratio test) the complete model (including the main effects and their interaction) with the model without the interaction. Fisher’s exact tests with simulated p-value (based on 10⁸ replicates) were used to test the homogeneity of the distributions of genotypes between compartments (within each region), and of genotypes between regions (within each compartment).

In order to assess whether the sampled genotypes were spatially structured within and between compartments, the relationship between genetic and geographical distances was tested at all distances using a geostatistical method based on join counts²⁴ and permutation tests. This approach is well adapted to an exploratory spatial analysis of epidemiological data because no assumption or prior knowledge of the processes of disease spread is needed (e.g., relative importance of several transmission pathways, distance and direction of spread, definition of population units)^56,57. The genetic distance between two samples was fixed at 0 if the samples had the same genotype, and at 1 if their genotypes differed. This definition corresponds to the join count between elements of different classes of nominal data²⁴. In cases where two different genotypes were detected in the same tree, their geographical distance was set at 0 (and their genetic distance at 1). In the case of a single compartment with n samples, the geographical distances between the n(n − 1)/2 pairs of samples were first calculated. Then, for each calculated distance d, we computed the average genetic distance D_d between the k_d pairs of samples separated by a geographical distance less than or equal to d (i.e., within a radius d). The average genetic distance was defined as:

where h_d is the number of pairs of samples with different genotypes among the k_d pairs. The confidence intervals (here, at level α = 0.05) were obtained from N (here, N = 10,000) random permutations of the genotypes of the n samples. We calculated the N average genetic distances within each distance d, and the lower (respectively, upper) limit was defined as the genetic distance with rank Nα/2 (resp., N(1 − α/2)) among the N random genetic distances. A significant reduction in genetic diversity at the beginning of the curve (i.e., for the smaller radii) is expected when genotypes are spatially clustered, and the distance at which this reduced genetic diversity becomes non-significant indicates the spatial extent of genetic similarity among samples. Significant genetic distances are interpreted as false positives when non-significant genetic distances are observed at shorter geographical distances (except when these shorter distances are associated with a very low statistical power, i.e., wide confidence envelopes). Considering the cumulative number of pairs separated by a distance less than or equal to d, rather than the number of pairs falling in distance classes defined by intervals, provides more powerful tests and more stable curves.

When d is equal to the maximum distance d_max between two samples, we have:

and

where n_i is the number of samples with genotype i and the summation is over all the genotypes. Thus, the value of ({D}_{{d}_{max}}) is:

which is Simpson’s diversity index. D = 0 if all the samples have the same genotype, and D = 1 if all the samples have different genotypes. Since ({h}_{{d}_{max}}) does not change when the genotypes are permuted, the lower and upper limits of the confidence interval are equal to D when d = d_max. When d < d_max, D_d can be considered as Simpson’s diversity index restricted to the pairs of samples separated by a geographical distance less than or equal to d.

In the case of two different compartments with n₁ and n₂ samples, a similar procedure was applied to the n₁n₂ pairs consisting of one sample of each compartment with the statistics:

where ({h{prime} }_{d}) and ({k{prime} }_{d}) have the same definition as h_d and k_d, except that the two samples belong to two different compartments. However, for the computation of the confidence intervals, only the genotypes of the less structured compartment were randomly permuted to prevent false positive tests caused only by breaking the structure of the most structured compartment by permutation⁵⁸. When the less structured compartment was also significantly structured, the tests were interpreted conservatively, i.e., interpreting the points bordering the limits of the confidence envelope as not being statistically significant. When d = d_max, the value of ({D{prime} }_{{d}_{max}}) is:

where n_1i and n_2i are the numbers of samples with genotype i in each of the two groups. D′ = 0 if the two groups have the same unique genotype, and D’ = 1 if the two groups have no common genotype.

Source: Ecology - nature.com