Pooled samples and eDNA-based detection can facilitate the “clean trade” of aquatic animals

Individual-level sampling

The probability of obtaining x infected individuals (D⁺) in a sample of size n taken without replacement from a population of size N, of which d are infected is described by a hypergeometric distribution⁸¹:

However, diagnostic tests are rarely perfect. Infected individuals are correctly detected with probability Se (diagnostic sensitivity) and uninfected animals correctly test negative with probability Sp (diagnostic specificity); false negatives and false positives occur with probabilities 1 − Se and 1 − Sp, respectively. Cameron and Baldock⁸¹ extended the hypergeometric model to include imperfect tests, such that the probability of observing x positive tests (T⁺) is:

Often our goal is to determine the probability of at least one positive sample, given particular parameter values. Consider a consignment of N = 100 salamanders, some 3% (d = 3) of which are infected, screened with individual swabs with a diagnostic sensitivity of Se = 0.8, matching the assumption in the EU regulations⁷⁰, and perfect specificity (Sp = 1). We see that the probability of detecting at least one of these infections is, using the equivalence P(T⁺ ≥ x) = 1 − P(T⁺ = 0):

Note that the part involving specificity simplifies to 1 when Se = 1. Because x = 0, j is always zero and so this simplifies to:

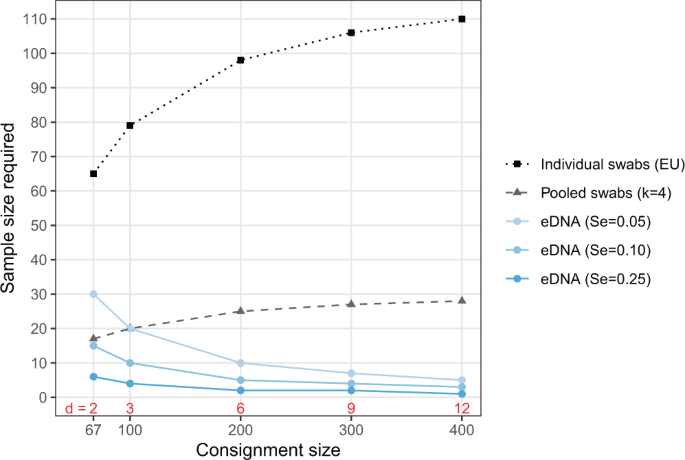
One can then try values of n such that P(T⁺ ≥ 1) ≥ 0.95 or any other threshold surveillance sensitivity. In this scenario the threshold is met when n ≥ 79. While this calculation can be done by hand, it becomes quite tedious. Using the R code found below the same calculation can be achieved with pooledHyp_Atleast1(d=3, N=100, m=79, k=1, Se=0.8, Sp=1). Note that that this function is written for pooled samples (see next subsection), but we can use it for individual samples with m = n “pools” (=samples) of size k = 1.

Pooling individual-level samples

When the n samples are divided into m groups of size k = n/m, which are then tested as pools, the probability that x of the m pools contain an infected individual in them (Pool⁺) is described by the “pooled hypergeometric” of Theobald and Davies²⁴:

for max[0, m − (N − d)/k] ≤ x ≤ min(m, d).

This formula can be extended to include false negatives and false positives in a manner analogous to Cameron and Baldock⁸¹, where the probability of observing x positive tests (({T}_{pool}^{+})) for the m pools is:

It is important to note that this formulation assumes diagnostic sensitivity and specificity are not influenced by the composition of a pool. A pool is equally likely to test positive if one or all of the individuals within it are positive, or if the pool is comprised of few or many samples. This assumption may be questionable for large pools, but may be reasonable with small k.

Returning to the example of a consignment of N = 100 with Se = 0.8 and Sp = 1, but now pooling swabs into groups of size k = 4 and assuming that the m pools is greater than the d = 3 infections, we can find the probability of at least one pool testing positive as:

but with the double summation this is rather unwieldy to solve by hand. Rather one can use the code, pooledHyp_Atleast1(d=3, N=100, m=20, k=4, Se=0.8, Sp=1), to find that P(T⁺ ≥ 1) ≥ 0.95 when m ≥ 20.

Environmental DNA

Let us assume that target eDNA is well mixed in the water. We can then use a binomial to describe the distribution of positive eDNA tests (({T}_{eDNA}^{+})) because taking one sample does not affect the probability of detection in subsequent samples. Retaining the definition of sensitivity as the probability of detecting one infection if present (i.e., (Se=P({T}_{eDNA}^{+}|d=1))), we obtain the following expression for the probably of observing x positive samples:

Note that because each eDNA sample collects material from all d infected individuals in the population, success is defined in the binomial as the probability of a positive eDNA sample [1 − (1 − Se)^d], ignoring false positives, rather than the probability a sample includes an infected individual, as is the case when using the binomial to describe detection probabilities with individual samples taken with replacement. Multiple infected individuals in a population simply increase the amount of target eDNA to be detected and thus the effective sensitivity of the eDNA test. Both sensitivity and specificity are assumed to be constant and independent of the N − d uninfected animals in the population.

Finding the number of replicate eDNA samples to ensure (P({T}_{eDNA}^{+}ge 1)ge 0.95) is rather simpler in this model. If we assume there are d = 3 infected individuals in a consignment (the size of which does not enter the equation, and a very low sensitivity, Se = 0.05, but perfect specificity, Se = 1, we can the probability that at least one sample tests positive:

Notice that both the binomial terms and the first term in brackets simplify to one since x = 0; in other words, we only need to subtract the probability that all n samples test negative from one. (P({T}_{eDNA}^{+}ge 1)ge 0.95) when n ≥ 20. While this is simple to calculate by hand, the code, eDNA_Atleast1(d=3, m=20, Se=0.05, Sp=1) produces the same result.

The quantitative nature of detection

Any test that reacts directly with a pathogen (e.g., pathogen DNA or antigens) or host responses (e.g., antibodies) is necessarily dose-dependent. Focusing on DNA-dependent detection methods (e.g., PCR), let us assume that every copy, C, of the target DNA sequence in a sample has a small, fixed probability of causing a positive result in a reaction, ϕ. The probability of a positive test result can then be described by a “single-hit” model^82,83:

which results in a typical dose-response relationship (Fig. 3). (A logistic relationship between P(T⁺) and log(C), which is commonly used in studies of analytic sensitivity, yields similar results, but requires an extra parameter.) If the C copies come from a single infected individual, then this function describes diagnostic sensitivity. The magnitude of C in a sample can therefore have a strong influence on sensitivity. As noted in the main text, one would expect greater variation in C with eDNA sample than with individual-level samples because eDNA is not collected directly from an animal, but from the environment, which can also play a role (although external swabs are also influenced by the environment). A simple model is useful in clarifying the factors that likely determine the number of target copies in an eDNA sample.

In this model, the number of copies of target eDNA in a sample increase as the d infected individuals shed into the water at rate ψ, some portion, α, of which ends up in each eDNA sample, and decrease as eDNA degrades at rate δ:

The solution is:

where C₀ is the initial concentration in the water (the first term on the right-hand side is zero when C₀ = 0). The solution asymptotes to C^* = ψdα/δ over time at a rate dependent upon δ. Substituting the equilibrium solution into the single-hit model (Eq. (11)), one can see that detection probability depends on these rates in a straightforward way:

While this model has several terms, they have clear biological meaning and could be estimated from experimental data^84,85,86. Moreover, they enter the model as a product, with equivalent effects, at least at equilibrium. That is, doubling the volume of water collected in an eDNA sample is the same as doubling the number of infected individuals or halving the decay rate. This model also provides a way to link the many factors that can affect eDNA-based detection via their influence on target copy number, C (e.g., degradation, δ, is likely temperature-dependent⁸⁶), or PCR efficiency (e.g., ϕ might be a function of pH and environmental inhibitors²⁹).

R code for sample size calculations

The pooled hypergeometric distribution of Theobald and Davies²⁴ can be implemented in R using the “big integer” versions of multiplication and the binomial expansion found in the gmp package⁸⁷ for greater precision:

pooledHyper <− function(x, d, N, m, k){

i = 0:x

as.numeric(

gmp::mul.bigq(gmp::chooseZ(m, x),

sum((−1)^i * gmp::chooseZ(x,i) * gmp::chooseZ(N-d, (m-x+i)*k)/

gmp::chooseZ(N, (m-x+i)*k)

)

)

)

}

This is then extended to include sensitivity and specificity, as in Eq. (7):

px_pooledHyper<− function(x, d, N, m, k, Se, Sp,…) {

# check inputs

if(x>m) stop(“x is greater than m (number of pools)”)

if(m*k>N) stop(“individuals sampled (m*k) is greater than population size (N)”)

stopifnot(Se<=1, Se>=0, Sp<=1, Sp>=0, length(x)==1)

innerSums <− 0

for(y in 0:m){

j<− 0:min(y,x)

innerSums[y+1] <- pooledHyper(x=y, d=d, N=N, m=m, k=k) *

sum(dbinom(j, size=y, prob=Se) * dbinom(x-j, size=m-y, prob=(1-Sp)))

}

sum(innerSums) # return sum of inner summations

}

Note that when k=1 the “pools” are individual samples, as in Eq. (6). A wrapper function can then be used to find the probability of at least one sample or pool of samples testing positive:

pooledHyp_Atleast1<− function(d, N, m, k, Se, Sp,…){

1-px_pooledHyper(x=0, d=d, N=N, m=m, k=k, Se=Se, Sp=Sp)

}

Equation (9) for eDNA can be implemented in R as:

px_eDNA <− function(x, d, n, Se, Sp){

# check inputs

stopifnot(Se<=1, Se>=0, Sp<=1, Sp>=0)

choose(n,x) * (1 – (1-Se)^d+((1-Se)^d)*(1-Sp))^x * (((1-Se)^d)*Sp)^(n-x)

}

A wrapper function is then used to find the probability of at least one eDNA samples testing positive:

eDNA_Atleast1<− function(d, m, Se, Sp=1,…){

1-px_eDNA(x=0, d=d, n=m, Se=Se, Sp=Sp)

}

Source: Ecology - nature.com