Potential sex-dependent effects of weather on apparent survival of a high-elevation specialist

Study site and the capture-recapture data set

From June 2003 to June 2017, 671 snowfinches were caught in the Apennines, within the Gran Sasso and Monti della Laga National Park, Italy, specifically within an area of 3 km² around Campo Imperatore (42°27 N, 13°34 E, 2200 m asl, see⁴⁸). Birds were captured all year round, using mist nets and nest traps (Table 3). Number of days with snowfinch capturing ranged between 41 and 55 per year. On average, 48 field days took place between April and October, and 4 between November and March. The positioning and length of nets used for trapping, and the time spent trapping per day could not be standardised because of the highly variable spatial behaviour of the birds and the variable weather conditions.

Snowfinches were marked with individual metal rings and, if possible, their age and sex were identified according to Strinella (2013)⁵⁹. Of the 671 individuals captured, 101 were marked as nestlings and 570 as fully grown individuals. Almost a quarter of the individuals (157 individuals) were identified as males, 104 as females, whereas for 410 individuals (61%) sex could not be identified (Table 4). Of the 671 marked individuals, 138 were later recaptured between 1 and 6 times.

Bird capturing and marking was authorised by the Institute for Environmental Protection and Research ISPRA (ES, licence CNI ISPRA no. 0114). Capturing and marking were carried out in accordance with guidelines and regulations of ISPRA.

Weather data

We obtained data on daily minimum and maximum temperatures (°C) and precipitation (mm per day) from two local weather stations (Assergi: 42°24′N 13°30′E, 992 m asl; and Castel del Monte: 2°22′N 13°43′E, 1346 m asl; Ufficio Idrografico e Mareografico Regione Abruzzo) for the years 2003 to 2017. Daily minimum and maximum temperature were highly correlated (Pearson’s correlation r = 0.93). We used the average between the minimum and maximum temperature of both stations as a measure of average daily temperature that is sensitive to extreme temperature values. Daily precipitation was summed over the two stations in order to obtain a measure of precipitation in the study area. We then averaged daily temperature and precipitation over the summer months (June to September) and over the winter months (November to March) for each year. These four weather variables were used to predict annual apparent survival (from summer to summer).

Precipitation in winter correlated positively with precipitation in summer (Pearson’s correlation r = 0.50). In summer, temperature correlated negatively with precipitation (r = −0.39). Weak positive correlations existed between winter temperature and precipitation in summer (r = 0.27), and precipitation in winter (r = 0.15), respectively. All other correlations were weaker than 0.1. Over the course of the study period, average summer temperature did not show any trend, whereas average winter temperature showed a weak positive trend (Fig. 4).

Figure 4

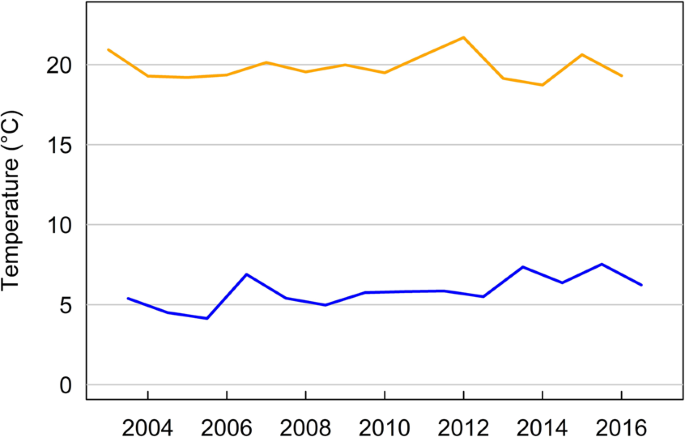
Average summer and winter temperature for each year of the study period. Summer temperature is the average temperature for the months June to September, winter temperature is the average between November and March.

Full size image

We did not consider weather variables during the breeding season because most birds were captured during or shortly after the breeding season (Table 3). Consequently, the length an individual is exposed to spring conditions during its first year after marking depends on the date of marking. We only included weather variables that could unambiguously be assigned to one summer to summer interval.

Survival models

General model structure

We used mark-recapture models^81,82,83,84 that we applied to two different temporal aggregations of the mark-recapture data set. The first analysis aimed at measuring average annual apparent survival, and investigating correlations between weather variables and annual apparent survival. In the second analysis, we described seasonal patterns of apparent survival probabilities. The general model structures in both analyses were equal but they differed in the length of the time intervals (years vs. 4-months periods) and the predictors for survival (see below). For the first analysis, we aggregated the data in annual time intervals (1st January – 31st December; mean capture date within this interval is 30th June). For the second analyses, four-month time intervals were used. For the annual data, time interval (t) was one year (of 15 years in total), and for the seasonal data, time interval (t) was four months (of 43 4-months periods or “seasons” in total).

The observations ({y}_{it}), an indicator of whether individual (i) was recaptured during time interval (t), were modelled as a Bernoulli variable conditional on the latent state of the individual birds ({z}_{it}) (0 = dead or permanently emigrated, 1 = alive and at the study site). The probability (P({y}_{it}mathrm{=1)}) is the product of the probability that an alive individual is recaptured, ({p}_{it}), and the state of the bird ({z}_{it}). Thus, a dead or permanently emigrated bird cannot be recaptured, whereas for a bird alive during time interval (t) the recapture probability equals ({p}_{it}):

The latent state variable ({z}_{it}) is a Markovian variable with the state at time (t) being dependent on the state at time (t-1) and the apparent survival probability ({Phi }_{it}):

We use the term “apparent survival” to indicate that the parameter (Phi ) is a product of site fidelity and survival. Thus, individuals that permanently emigrated from the study area cannot be distinguished from dead individuals.

In both models, the parameters (Phi ) and (p) were modelled as sex-specific. However, for 61% of the individuals, sex could not be identified, i.e. sex was missing. Ignoring the individuals with missing sex would most likely lead to a bias because they were not missing at random. The probability that sex can be identified is increasing with age and most likely differs between sexes. Further, in our data, the probability that sex could be identified varied across the study period because different methods (genetics, plumage, breeding patch) were used in different years, and sex identification literature became available during the study period⁵⁹. As a consequence, we cannot use our data to estimate the sex-specific probability of identifying the sex of an individual⁸⁵. However, we can include the missing sexes using a mixture model structure similarly to Pledger (2000)⁸⁶ who introduced a mixture model for unknown classes. In our case, for part of the individuals, the class (sex) was known. We imputed the sex assignment for non-identified individuals using a categorical distribution with a uniform (Betamathrm{(1,1)}) distribution for the probability of being a male ({q}_{i}mathrm{[1]}):

where, for every non-identified individual, ({{bf{q}}}_{i}) is a vector of length 2, containing the probability of being a male and a female, respectively. The sex of each non-identified individual was therefore assumed to be male or female with probability ({q}_{i}mathrm{[1]}) and ({q}_{i}mathrm{[2]}=1-{q}_{i}mathrm{[1]}), respectively. A uniform distribution between 0 and 1 was assumed for ({q}_{i}mathrm{[1]}). In this way, no specific sex was assigned to these individuals, but their data was used for the survival estimates preventing them to be overestimated. Indeed, the posterior distributions of the ({q}_{i}mathrm{[1]}) were close to a uniform distribution in all models. Therefore, we do not present them in the results.

In addition, we fitted all models without the mixture structure to a reduced data set including only individuals with identified sex and only the re-captures after their sex could first be ascertained⁸⁷. Except for 5 individuals, all individuals were adult when their sex was ascertained. These 5 individuals were excluded from the analyses on the reduced data set. In such a reduced data set, individuals that show clear sex-specific characteristics and that are strong enough to live long will be over-represented. Consequently, the results may not be representative for the snowfinch population in the Apennines. On the other hand, also the full data set may not be a random sample of individuals because inexpert or high active individuals are more likely to be captured by mist-nets than experienced or less active individuals^88,89. Therefore, we present the results from the analyses of both the full and reduced data sets.

Annual apparent survival models

We used seven different models for annual apparent survival that differed in their temporal structure of apparent survival (Table 1). In the first model, we assumed constant apparent survival over time, but included different apparent survival for age and sex classes (3 levels: first year birds, adult males and adult females):

Model 1: ({Phi }_{it}={a}_{t,agemathrm{}.sex[it]})

In the second model, we included a sex-specific random year effect

Model 2a: (logit({Phi }_{it})=a{0}_{agemathrm{}.sex[it]}+{gamma }_{sex[i]t}) with ({gamma }_{sex[i]t} sim Normalmathrm{(0,}sigma )).

The third model is similar to model 2a but it includes for each age and sex class a separate apparent survival for the first year after first capture (first occasion). It thus estimates for both sexes two adult apparent survival, one during the first year after the first capture and one during the second and later years after the first capture. Because juveniles become adults after one year, the models include only one apparent survival for juveniles.

Model 2b: (logit({Phi }_{it})=a{0}_{agemathrm{}.sex[it],firstoccasion[it]}+{gamma }_{sex[i]t}) with ({gamma }_{sex[i]t} sim Normalmathrm{(0,}sigma )), where the variable firstoccasion contains a 1 for the first occasion and a 2 for later occasions.

In the following four models, we modelled annual apparent survival to be linearly related to average summer and average winter temperature (summertemp, wintertemp, models 3a, 3b, 23b, and 4). In the last model (model 4), we also included precipitation (summerprec, winterprec) as predictors. We estimated different effects of temperature and precipitation on apparent survival for juveniles, adult males and adult females:

Model 3a: (logit({Phi }_{it})=a{0}_{agemathrm{}.sex[it]}+a{1}_{agemathrm{}.sex[it]}summertem{p}_{t}+a{2}_{agemathrm{}.sex[it]}wintertem{p}_{t})

Model 3b was similar to model 3a but included separate apparent survival and separate correlations between temperature and apparent survival during the first year after first capture and during the second or later years after the first capture.

Model 3b: (logit({Phi }_{it})=a{0}_{agemathrm{}.sex[it],firstoccasion[it]}+a{1}_{agemathrm{}.sex[it],firstoccasion[it]}summertem{p}_{t}+a{2}_{agemathrm{}.sex[it],firstoccasion[it]}) (wintertem{p}_{t})

Model23b combines the random year structure of model 2, the linear relationship with summer and winter temperature of model 3, and it also includes separate apparent survival for the first and later years after the first capture. However, in model 3b the correlations with temperature variables separately for first and later years after the first captures could not be estimated well (low sample size). Therefore, in model 23b we estimated only one correlation between apparent survival and each of the temperature variables and assumed that this correlation was the same for first and later years after the first capture.

Model 23b: (logit({Phi }_{it})=a{0}_{agemathrm{}.sex[it],firstoccasion[it]}+a{1}_{agemathrm{}.sex[it]}summertem{p}_{t}+a{2}_{agemathrm{}.sex[it]}wintertem{p}_{t}+{gamma }_{sex[i]t}) with ({gamma }_{sex[i]t} sim Normalmathrm{(0,}sigma ))

In the last model, we included summer and winter temperature and summer and winter precipitation as predictors for apparent survival.

Model 4: (logit({Phi }_{it})=a{0}_{agemathrm{}.sex[it]}+a{1}_{agemathrm{}.sex[it]}summertem{p}_{t}+a{2}_{agemathrm{}.sex[it]}wintertem{p}_{t}+a{3}_{agemathrm{}.sex[it]}summerpre{c}_{t}+a{4}_{agemathrm{}.sex[it]}winterpre{c}_{t})

In all models, annual recapture probability was modelled for each year and sex independently: ({p}_{it}=b{0}_{t,sex[it]}). Because all individuals were at least one year old when they can be recaptured for the first time, we did not include age as a predictor for recapture probability.

Uniform prior distributions were used for all parameters with a parameter space limited to values between 0 and 1 for probabilities. A normal distribution with a mean of 0 and a standard deviation of 1.5 was used for the intercept (a0), and for (a1), (a2), (a3), and (a4) a standard deviation of 3 was used.

Seasonal survival model

We assumed that four-month survival differed between age and sex classes (juveniles, adult male, adult female), and seasons (winter: December – March, breeding: April – July, summer: August – November), ({Phi }_{it}={a}_{sexmathrm{}.age[i],season[t]}). Independent, and slightly informative prior distributions ({a}_{sexmathrm{}.age[i],season[t]} sim Betamathrm{(3.6,1.2)}) were used. This prior gives 95% of the mass to values between 0.33 and 0.99 and has a median of 0.79. An average survival of 0.79 over 4 months corresponds to an annual survival of 0.49. By choosing a prior distribution with a mean corresponding to approximately the overall mean of the data we make sure that estimates for specific seasons deviating from the overall mean show information that is inherent to the data. Using a uniform prior, (Betamathrm{(1,1)}), with a mean of 0.5 would result in estimates close to 0.5 for seasons with a small sample size, i.e. during winter, which would bias the conclusions on seasonal differences in seasonal survival. Recapture probability was assumed to depend on season, sex and year using the logit link function and assigning a normal distribution to the year effects:

Independent normal prior distributions were specified for the average logit-transformed recapture probabilities,

Model fitting and predictive model checking

We used Hamiltonian Monte Carlo as implemented in Stan⁹⁰ to fit the models to the data. We simulated 4 Markov chains of length 2000 and used the second half of each chain for the description of the posterior distributions of the model parameters.

Convergence and mixing of the Markov chains were assessed by the metrics and diagnostic plots provided by rstan⁹¹ and shinystan⁹² packages, i.e. no divergent transition, number of effective samples above 1000, Monte Carlo errors below 10%, and R-hat value below 1.01.

In order to assess the goodness of fit, we used R 3.6.1⁹³ to simulate from the model 1000 times new capture histories for each individual in the data. For every draw we used another set of parameter values from the simulated joint posterior distribution of the model parameters (that was generated by Hamiltonian Monte Carlo in Stan, as described above). These 1000 new data sets look like the model “thinks” the data should look like³⁸. For every new data set, we extracted the number of individuals captured exactly once and the number of individuals captured at least three times. We compared these two statistics between the 1000 new data sets and the observed data.

Source: Ecology - nature.com