State-space models reveal a continuing elephant poaching problem in most of Africa

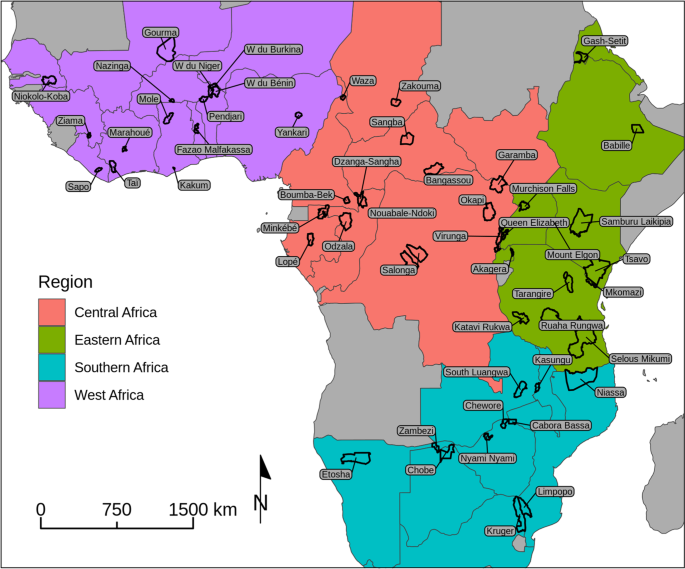
Study areas

We used data from 53 African MIKE sites that began reporting prior to 2010 (Fig. 1). Additional sites in Asia as well as African sites added to the program in 2018 were not considered here. MIKE sites tend to be protected areas, though some sites are unprotected or include both protected and unprotected areas. The 53 sites average 9,863 km² in area (range: 175–51,027 km²) and are divided into four regions (Fig. 1). Habitats on MIKE sites are varied and include savannahs, grasslands, tropical forests, and a variety of other vegetation types. In our analyses, we did not attempt to distinguish between sites with forest or savannah elephants. Forest elephants predominate in MIKE’s Central Africa region, though a few sites in this region hold savannah elephants.

MIKE data

MIKE data were made available by CITES at http://cites.org/eng/prog/mike/data_and_reports. Each MIKE site reports annual totals of the number of carcasses of all origins encountered and the number of illegally killed carcasses encountered. The program utilizes strict criteria for determining a carcass’ cause of death²². In our analyses, we used data from 2003–2018; we excluded data from a few pilot sites in 2002. As mentioned above, no data exists for many site-year combinations, and some MIKE sites have few years with data. To accurately estimate trends in PIKE, we arbitrarily restricted the dataset to sites with at least 4 years with data for 2003–2011 and 4 years with data for 2011–2018. We used 2011 as a dividing point because of reports that 2011 was an inflection point for elephant poaching rates, with distinct trends before and afterwards^6,7. Thus, good estimates of trends in PIKE require multiple observations before and after 2011. We tested how these sample-size restrictions affected our results, as discussed below.

Elephant population estimates

To estimate PIKE by region or for the continent, we had to weight PIKE estimates from individual sites. The MIKE program weights individual sites by the number of carcasses reported¹³. As noted above, carcasses reported are only weakly related to elephant population size and more likely reflect search effort as well as rates of poaching and natural mortality. Instead, we weighted site PIKE estimates by live-elephant population size. This should allow for better inferences about regional and continental poaching levels because the resulting PIKE estimates should be representative of the entire region or the continent. We obtained elephant population estimates for MIKE sites from four sources (see Supplementary Table S1): published survey reports, unpublished survey reports, the African Elephant database²³, and African elephant status updates from IUCN^24,25. For each survey, we examined study area maps to ensure that survey boundaries were congruent with MIKE site boundaries. Where necessary, we excluded survey strata outside MIKE boundaries from population estimates.

MIKE data are reported annually, but elephant surveys were generally less frequent. Weighting by elephant population size requires estimates for each site and year. Thus, for each site, we used linear interpolation to estimate population sizes between surveys. For years prior to the earliest available survey, we used the earliest survey estimate. For years after the latest elephant survey, we used the latest survey estimate. If only a single elephant population estimate was available, we used that estimate for all years. In our sample, there was a positive correlation between the number of elephant population estimates and the mean population size (r = 0.45). This means that fewer interpolated estimates were generally needed for the sites with the largest weights in the analysis.

State-space models

We used state-space models to estimate the unobserved, “true” PIKE for each site and year while accounting for missing data and smoothing over fluctuations due to sampling error. The state-space model has two components: an observation model, which treats observed PIKE as a noisy sample of the state, and a process model, which treats change in the state over time as a parametric process. To avoid confusion with observed PIKE values, we refer to the state estimates as “sPIKE”; like PIKE, sPIKE is also on a probability scale. The observation model was a draw from a binomial distribution, with probability equal to sPIKE so that

({K}_{i,t} sim {rm{binomial}}({C}_{i,t},{s}_{i,t}))

where s is sPIKE, K is the number of illegally killed carcasses, and C is the total number of carcasses reported for site i and year t. We modeled change in sPIKE over time as a random walk on a logit scale as

Here, ({{epsilon }}_{i,t}) is the “disturbance,” the change in the state from year to year. Larger values of ({sigma }_{i}^{2}), the process error, allow for more rapid change in the state and more “wiggle” in sPIKE estimates. We estimated process error separately for each site, as discussed below.

The state-space model partitions variance in PIKE between the state process and the observation process. As a result, observed values of PIKE, K/C, will deviate from sPIKE due to binomial sampling. At the same time, sPIKE should be a more accurate index of poaching levels because it is relatively insensitive to outliers and random fluctuations in observed values. Another advantage of the state-space model is the ability to predict sPIKE in years when data was missing for a site, by estimating disturbances from equations (2) and (3). Regional and continental estimates of sPIKE use estimates from all sites in all years so that resulting values are not biased by missing data.

We used the extended Kalman filter to fit the binomial state-space models. The Kalman filter is an algorithm for estimating the underlying state from noisy observations¹⁶. In practice, the Kalman filter optimally partitions the variance in observations between the state and observation processes. The extended Kalman filter uses Taylor-series expansion to approximate the binomial distribution as a linear equation, allowing the model to be fit by maximum likelihood. We made inferences from smoothed estimates of the state¹⁶.

We ran our models using the KFAS package²⁶ in Program R²⁷. The Kalman filter can be used with multivariate time series, which combine multiple sites. In such models, the process error term is a covariance matrix, so that correlations between sites can be explicitly modeled. We initially tested multivariate models fit by region, with the process error modeled as an unstructured covariance matrix. This formulation allowed for correlations between sites in the random walk disturbances, as might be occur if sites follow parallel trends over time. We compared the multivariate models with models in which process errors were independent for each site. Per Akaike’s Information Criterion, models with independent disturbances by site were strongly preferred over models with correlated disturbances. Thus, we made inferences from models in which disturbances were uncorrelated between sites.

To validate models, we assessed model residuals for spatial and temporal autocorrelation using the ncf package²⁸ in R. As a measure of model fit, we computed the correlation between model predictions and actual PIKE values. To test how our minimum sample size requirements affected our results, we used the state-space model to predict continental sPIKE for minima of 2–5 years of data for 2003–2011 and for 2011–2018.

Regional estimates and trends

We used the site-wise sPIKE estimates to assess trends in poaching for the four regions and for the entire continent. For each year, we calculated regional or continental sPIKE as the weighted mean of the site estimates, with weight equal to estimated elephant populations. Weighting by the number of live elephants is advantageous because the resulting sPIKE estimates should be an index of the overall proportion of elephants poached in the given region. Accordingly,

Here, r is the regional or continental sPIKE estimate, w is the weight, E_i,t is the estimated number of live elephants, and N is the total number of sites in the given region or continent. We computed variances of regional sPIKE estimates on a logit scale as

for two reasons: first, to allow for the normal approximation to hold in calculating confidence intervals, and second, because our state-space models estimate variances for sPIKE on the logit scale. Per Oranje²⁹, we calculated 95% confidence limits on regional sPIKE on the logit scale and then back transformed the estimates to the probability scale as

To assess trends, we used linear regression, with regional or continental sPIKE estimates as the dependent variable and year as the independent variable. Because earlier studies showed that poaching peaked in 2011, we conducted separate regressions for 2003–2010 and for 2011–2018 for each region. To account for error in the dependent variable in the regression, we used the feasible generalized least squares method³⁰. When the estimated error due to the variance in sPIKE was small, this method was equivalent to inverse-variance weighted least squares regression. To reduce the probability of type-I error, we used Bonferroni correction on the significance levels of the regression coefficients for a family-wise error rate of 0.05.

Simulations

To test the accuracy of the state-space models, we used simulations with known “true” PIKE values. We ran two sets of simulations, each of which included 100 simulated carcass datasets with sample size identical to that of the MIKE dataset—16 years of observations and 38 sites. In the first set of simulations, we assumed a monotonic trend in actual PIKE values (hereafter “aPIKE”) at each site. For each site, we drew a random starting value for year 1. Subsequent aPIKE values followed a linear trend on a logit scale, with random deviations from the trendline for each year. Accordingly, for site i,

Here, a is aPIKE, β is the linear trend in aPIKE on a logit scale, and (varepsilon ) is the random departure from the trendline. In the simulations, numbers of illegally killed carcasses were randomly drawn for each site and year from binomial distributions with probability = aPIKE and sample size equal to the observed total number of carcasses in the MIKE dataset for that site and year. To make the simulated dataset match the MIKE data, we removed site-year combinations from the simulated dataset that were missing for the actual data. This allowed us to learn how well the state-space model compensated for missing data.

The second set of simulations utilized random values of aPIKE for all sites and years, with no underlying trends. Accordingly,

({a}_{i,t} sim {rm{U}}(0,1))

We drew numbers of illegally killed carcasses with binomial draws from the aPIKE values as above. Again, the simulated datasets included only site and year combinations that were not missing in the MIKE dataset.

For each simulated dataset, we used state-space models to estimate sPIKE for each site and year, as described above for the MIKE data. To measure the accuracy of the models, for each set of simulations, we computed the root mean squared error (rmse) of sPIKE for each site and year and averaged the rmse over all estimates. We also calculated continental sPIKE estimates for each simulation and computed the mean rmse over the years for those estimates.

Source: Ecology - nature.com