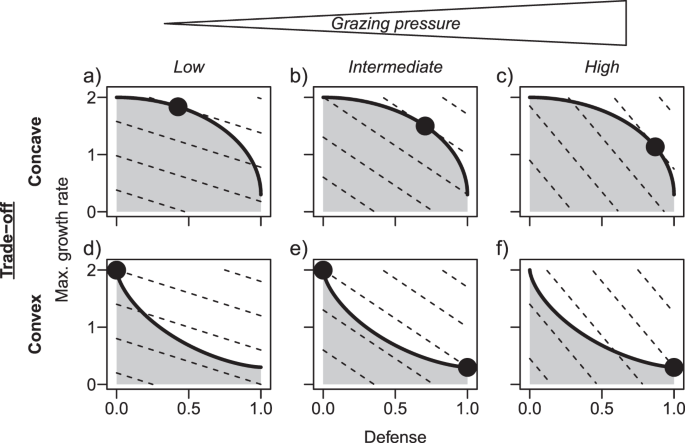
The 36 dominating phytoplankton morphotypes in Lake Constance faced a concave trade-off between defense and maximum growth rate. We found that the community average values of defense and maximum growth rate showed opposed seasonal dynamics. We did not observe distinct seasonal dynamics in the community average phosphate affinity, but morphotypes with a rather low growth rate relative to their defense level often had a relatively high phosphate affinity. Theory predicts that concave trade-off curves promote species with intermediate strategies (Box 1 and Fig. 1). Our data support this prediction as intermediately defended morphotypes with intermediate to high maximum growth rates constituted the largest proportion of total annual phytoplankton biomass. Trait shifts in the phytoplankton community along the concave trade-off curve were exactly in line with seasonal changes of the environmental conditions. The model predicted a shift toward higher defense levels at the cost of lower maximum growth rates with increasing grazing pressure from spring to summer, as found in the data, and revealed low fitness differences of persisting species along the trade-off curve. Assuming a hypothetical convex trade-off in the model, for comparison, produced biomass-trait distributions were qualitatively different from the observations. Hence, our model results highlight the importance of quantitative knowledge on the shape of the trade-off.
The quantification of the trade-off was based on trait data provided by Bruggeman [35]. He obtained phytoplankton trait values from a statistical model, fed with a great quantity of lab trait measurements and phylogenetic relationships. He provided also quantitative information on model uncertainties, i.e., the standard errors of the trait estimates [35]. We consider these uncertainties to be minor compared with the measured trait range, not questioning the general pattern of a concave trade-off (Fig. S1b). The defense (edibility) values, used in Bruggeman’s statistical model [35], were almost entirely based on measurements of Lake Constance phytoplankton strains, sampled during the first part of our study period [44], and were tested for daphnids, the dominant herbivorous crustaceans in Lake Constance, which have a similar food spectrum as most of the other herbivores (see Methods). Hence, we argue that the concave trade-off between defense and maximum growth rate obtained from these trait data is adequate for the considered phytoplankton community in Lake Constance. Wirtz and Eckhardt [46] suggested a linear defense-growth trade-off for the same phytoplankton community, but they considered only seven species, missing several dominant ones. They were able to predict the seasonal dynamics of total phyto- and zooplankton biomass and of the community average trait values [46]. However, they did not consider the biomass distribution in the trait space and thus could not provide predictions on which species/trait combinations may dominate or co-occur. To adequately predict this biomass-trait distribution, the trade-off shape is important. By including trait data on many more than seven species, we found that the trade-off was concave and hence favored species with different intermediate defense levels, as observed.
Bruggeman [35] included also data on cell sizes. We found that defense correlated positively and maximum growth rate negatively with cell size (Fig. S3, Appendix 3), providing a potential mechanistic explanation for the existence of the defense-growth trade-off [47, 48]. However, other cell size-independent defense strategies are relevant as well, e.g., cell wall thickness, colony formation, toxicity and cell shapes, which introduce substantial scatter into the relationship between defense and size.
Our model showed that, for a concave trade-off curve, two very similar species can stably coexist (Figs. 5a and S7). This is in contradiction with theory predicting the survival of only one species (see Box 1 and Fig. 1a–c). The two species have intermediate strategies close to the fitness maximum and coexist based on stabilizing mechanisms arising from their slight difference in defense and growth [36]. However, this community is not evolutionary stable [49]. Given gradual evolution, we expect that one species would reach the exact fitness optimum via trait adaptation and outcompete the others for a concave trade-off curve [10, 12]. Even without evolution, such a coexistence would not last if a species exactly at the fitness maximum is initially present in the community. In line with our model results, Leibold [50] predicted a similar coexistence pattern based on a graphical approach, although his focus was not on the trade-off structure: Two very similar prey species coexisted in a food web with different prey species sharing one resource and one predator and a continuous transition occurred in the set of prey species persisting under gradually changing environmental conditions. With increasing system productivity, species with a higher defense level persisted [50], similar to the pattern in our study when increasing the grazing pressure. This indicates that he implicitly assumed a trade-off structure equivalent to the concave trade-off in our study. We argue that the behavior of communities in respect to coexistence (e.g., coexistence of similar intermediate strategies vs. different extreme strategies) and species replacement under environmental change may allow conclusions on the underlying trade-off structure.
The low trait variation maintained in the long-term model simulations is in contradiction with the empirical data showing a large trait variation, including species having intermediate strategies as well as specialized species (highly defended or fast-growing). The high number of species in such phytoplankton communities, exceeding the number of limiting factors (i.e., potential niches), is well known as the “Paradox of the Plankton” [21]. In the absence of stabilizing mechanisms arising from variation of interacting populations or environments in space or time [36], the number of coexisting species cannot exceed the number of limiting factors [51]. In line with that, our simple model, including only two niche dimensions (i.e., being defended or fast-growing), generated coexistence of maximal two species. Nevertheless, low fitness differences allowed for short-term co-occurrence of species in the model along and slightly below the concave trade-off curve (see green/orange region in Fig. 5a, b), a similar trait space where species persisted in the natural community (Fig. 3b). In contrast, feasible trait combinations well apart from the trade-off curve (low defense and low maximum growth rate) went quickly extinct in the model, implying a high fitness disadvantage. This provides an explanation for their absence in Lake Constance and in the whole data set of Bruggeman [35] (Fig. S1a).
According to modern coexistence theory [36], low fitness differences (as found along the trade-off curve) can form a fundamental basis for long-term maintenance of biodiversity: as then even slight stabilizing mechanisms (i.e., mechanisms slightly increasing negative intraspecific interactions relative to negative interspecific interactions) can lead to stable coexistence of many species. Fitness differences can be very low along a trade-off curve, if its shape is very similar to the shape of fitness isoclines [14, 52], e.g., for a nearly linear trade-off given linear fitness isoclines (Fig. 1). Stabilizing mechanisms, which overcome fitness differences and may help to explain the high trait variation observed along the trade-off curve, can be divided into: (1) niche differentiation along further trait axes, and (2) fluctuation-dependent mechanisms, like relative nonlinearity in competition and the storage effect [36].
Several trait dimensions, not considered in our model, may contribute to the biodiversity in the phytoplankton community, by further reducing fitness differences or by enabling niche differentiation. For instance, a high phosphate affinity is beneficial under strong nutrient depletion during summer and autumn. Although we found no clear increase of this trait on the community level during summer, it may explain the success of certain morphotypes. For example, the defended dinophytes (like Ceratium hirundinella and Peridinium sp., taxon number #4 and #27 in Fig. 3a) have very high phosphate affinities and constitute substantial biomass, despite their very high defense costs regarding the maximum growth rate (Fig. 3b). The undefended Rhodomonas ssp. (#29) also had a high phosphate affinity (Fig. 3a, b), which sheds light on its observed high biomasses and very regular occurrence in spite of its maximum growth rate not exceeding the one of intermediately defended morphotypes. In fact, we found a weak three-dimensional trade-off among defense, growth rate and phosphate affinity (Online Movie), though the negative correlation between the former two was the most striking pattern in the trait data (Fig. S2, Appendix 3).
Different light spectra and phytoplankton photopigmentation represent another important source for niche differentiation [17, 25]. For example, Rhodomonas spp. (#29) is able to use additional light spectra, based on the red accessory photopigment phycoerythrin allowing photosynthesis at greater depths, which is relevant year round due to vertical mixing and self-shading. The same holds for Cryptomonas spp. (#11) which also reached high biomasses irrespectively of its rather low maximum growth rate relative to its defense level (Fig. 3a, b). The cyanobacteria (Anabaena spp. and Oscillatoria spp., #1 and #24) also produce additional photopigments, which may compensate for their relative low maximum growth rates (Fig. 3a, b). Motility, in terms of swimming/floating toward light, can increase the performance with respect to light harvesting [17], which is relevant for e.g., the cyanobacteria showing buoyance regulation. Furthermore, vertical migration of some phytoplankton morphotypes, like Ceratium hirundinella (#4), enable exploiting additional nutrient sources from deeper water layers, when the water column is stratified during summer. Mixotrophy represents another possibility to obtain additional phosphate, which is relevant in Lake Constance [53]. The low phosphate affinities of bacterivorous mixotrophs as Dinobryon ssp. (#15) may partly explain the seasonally and interannually invariant signal in the community average phosphate affinity (Figs. 2d and S6) as they predominantly occur during summer and in later years. Diatoms seem to have maximal fitness regarding their defense and maximum growth rate, and are indeed present at high biomasses (Fig. 3a, b). However, they face disadvantages due to the production of shells, implying an additional silica demand and causing high sedimentation rates during stratified conditions, which leads to lower net growth rates than expected from their maximum growth rate. This helps to explain their success during early spring (Fig. 4a).
Relative nonlinearity in competition and the storage effect represent further stabilizing mechanisms, which may be relevant for our system and both depend on fluctuations in populations or environmental conditions (e.g., nutrient concentrations) [36]. Abrams [11] showed for a competition model that stable coexistence of two specialists using two different resources and one generalist is possible under asynchronous resource fluctuations. The species coexisted based on the relative nonlinearity in their resource uptake functions [51]. Such relative nonlinearity enabling stable coexistence has not been found for the type of predator-prey model considered here, but may be relevant when including additional resources (e.g., silica, light) with seasonally fluctuations. This can lead to coexistence of a high number of phytoplankton species, exceeding the number of limiting resources under nonequilibrium conditions [54, 55]. However, we did not include such seasonal forcing in our model simulations, but run different scenarios with constant environmental conditions mimicking distinct seasonal phases. Based on that, we obtained insights on the fitness landscape, that is, which trait combination would be favored during a certain seasonal phase and which species would be of low fitness (i.e., go quickly extinct in the simulation). The model purpose was not to reproduce the dynamics and the stable coexistence of many species across years in a distinct lake. This would demand a more complex modeling approach implementing, among others, periodical forcing of the abiotic environment (light, vertical mixing intensity, nutrient availability) and details like the overwintering strategies of phytoplankton, which goes beyond the scope of this article.
Lake Constance exhibits a pronounced seasonality (Fig. 2a, b). Our data demonstrate that the instantaneous fitness maximum gradually moves along the trade-off curve from fast-growing, intermediately defended species in early spring to slowly growing but more defended species in summer and then back in winter (Fig. S4, Appendix 3). Thus, different species along the trade-off curve have maximal fitness at different times of the year. This pattern of gradually moving fitness maxima is specific to concave trade-off curves (Fig. 1a–c) and is not expected for convex ones (Fig. 1d–f). Phytoplankton species form resting stages under unfavorable conditions, which buffers population losses [56]. This gives rise to storage effects [36], contributing to the maintenance of numerous phytoplankton species along the trade-off curve.
Lake Constance has successfully served as a model system for large open water bodies including marine ones [57]. It exhibits a typical seasonal plankton succession, driven by vertical mixing, grazing and nutrient limitation [22]. These environmental factors are also main drivers of marine phytoplankton, which is ecologically similar to freshwater phytoplankton and may face similar trade-offs [58]. Trade-offs between defense and growth are also relevant in terrestrial plant communities, for example grasslands [59]. Thus, our findings are likely relevant for numerous ecosystems. Furthermore, our results show that the information on trade-off shapes allows for an understanding of ongoing trait changes directly under field conditions.
Overall, the identification of the major trade-off and its shape provided a remarkable key to understand trait shifts and altering species composition in the phytoplankton community under seasonally changing environmental conditions. Although multiple trait dimensions likely play a role, our results showed that defense and maximum growth rate represent key traits in phytoplankton of Lake Constance, where grazers are known to strongly impact phytoplankton net growth [37]. A high maximum growth rate is beneficial at high resource concentrations, but also at low concentrations, when not coming at substantial costs of a lower nutrient uptake affinity. The maintenance of trait variation was likely promoted by low fitness differences along the concave trade-off curve. Low fitness differences allow coexistence by even slight stabilizing mechanisms arising from niche differentiation along multiple trait axes and fluctuations in environmental conditions, continuously moving favorable trait combinations along the concave trade-off curve. Our study successfully explained major trait dynamics based on a simple model, including only the interspecific defense-growth trade-off, and allowed to verify the theory on trade-off shapes in the field. In conclusion, quantifying trade-off shapes enhances our understanding of trait dynamics and variation in natural communities.
Source: Ecology - nature.com


