Probabilistic modeling to estimate jellyfish ecophysiological properties and size distributions

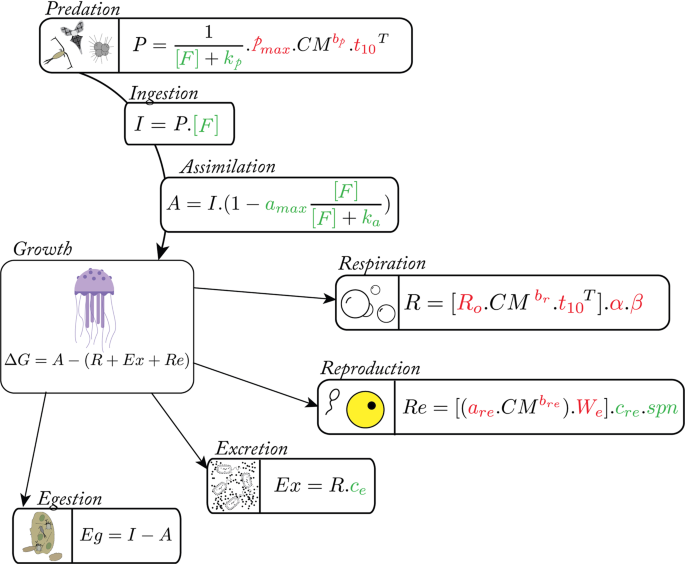
Conceptual model

To understand the role played by jellyfish for carbon cycling, it is essential to trace each physiological process where carbon is implicated. An ecophysiological 0-D model was built based on three forcing variables, which are temperature (T), food concentration (F) and initial jellyfish carbon mass (CM). The growth (G; gC.d⁻¹) of any organism depends on the balance between the quantity of assimilated preys (A) and losses due to respiration (R; gC.d⁻¹), excretion (Ex; gC.d⁻¹) and reproduction (Re; gC.d⁻¹). After ingestion (I; gC.d⁻¹), unassimilated predated preys are considered as egestion (Eg; gC.d⁻¹). In this way, the scope of growth and Eg could be expressed respectively by equations Eq. 1 and Eq. 2 below. Each variable was determined separately.

To estimate the assimilation rate, an estimation of ingested prey itself subject to the predation rate (P) and prey concentration (F) is necessary. The total amount of predated food is a function of an allometric relationship that depends on individual carbon mass (CM), temperature (T; °C) and food concentration, as follows:

where p_max is the maximum net feeding rate, t₁₀ the tenth root of the Q₁₀ which describes by how much rate changes with a 10 °C increase, and b_p is the regression coefficient. The parameters p_max, b_p, and t_10p were calibrated following the relationships between carbon weight and clearance rate defined for 8 different jellyfish species by Acuna, et al.⁶⁶ (Fig. S1). Michaelis-Menten kinetics were performed in the predation equation, with a half constant saturation of feeding rate (k_p). However, the parameters p_max and k_p are interconnected. To minimize the time needed for the new parameterization approach, we assumed that the most laboratory observations⁶⁶ corresponds to food saturating condition (i.e., two times higher than the maximum food concentration recorded in the in situ condition; F_sat = 0.00012 gC.L⁻¹) accordingly to which the relationship between p_max and k_p were identified, such as p_max = 0.1399.(1 + k_p/F_sat).

In this model, the ingestion rate is expressed by the simple product between prey concentration and predation rate, as follows:

However, the assimilation rate is different than the ingestion one and the model assumes that the fraction of food ingested and effectively assimilated decreases with increasing zooplankton concentration following a Holling type II Michaelis-Menten relationship:

where a_max is the maximum fraction of assimilated food and k_a is the half-saturation constant for assimilation.

To estimate the organic carbon losses due to the jellyfish metabolism, we considered four main processes: respiration, excretion, reproduction, and egestion rate. Many authors investigated jellyfish respiration rates^34,66 but we choose to adapt the approach of Lilley, et al.³⁴, which performed an allometric equation on P. noctiluca species such as:

where R_o is the theoretical respiration rate for 1 g CM individual at 0 °C, b_r is the allometric exponent for the effect of individual mass on respiration rate and t₁₀ is the tenth root of the Q₁₀ coefficient. To convert oxygen to energy units and then energy units to carbon units, two parameters α (J. μmolO₂^−1 67😉 and β (gC.J^−1 36;), were used respectively. The parameters R_o, b_r, and t_10r were calibrated according to log-log relationship between carbon weight and respiration rate obtained by Lilley, et al.³⁴ (Fig. S2).

Jellyfish excretion has been largely studied^10,58. DOC concentration from excretion activity was considered to scale with respiration rates, which is representative of the overall metabolic rates, as follows:

with c_e being the scalar factor.

Concerning the reproduction, when P. noctiluca is sexually mature, each individual spawning releases hundreds of eggs bound into mucus. In our model, eggs production was estimated thanks to the power-law relationship developed by Lilley, et al.³⁴ (Fig. S3) and two additional parameters c_re and spn, that characterize mucus (as the proportion of eggs carbon) and spawning frequency (spawn per day) respectively following the equation Eq. 8:

where a_re and b_re are coefficient parameters and W_e is the egg carbon mass³⁸. Sexual maturity allowing egg production was attained when jellyfish size reached 4 cm²⁹.

To estimate the contribution of POC_jelly to the carbon pump, the sinking speed (w; m.d⁻¹) and the remineralization rate (k; %.d⁻¹) were implemented in our model after estimation by laboratory experiments. The amount of carbon sequestered by jellyfish at a given depth was then modeled as follows:

In order to adapt the equations found in literature and switch easily between morphometric units, the model uses two conversions developed by Lilley, et al.³⁴. Thus, the jellyfish carbon mass represents 0.36% of the wet mass. Moreover, the wet jellyfish mass and carbon mass follow an allometric law with the size of P. noctiluca, such as:

with BD, WM, and CM representing respectively the bell diameter over lappets (cm), wet mass (g) and carbon mass (mg).

Model execution and observation data

To correctly represent growth and degrowth of P. noctiluca, model outputs were compared to our laboratory and in situ measurements as well as those carried out by Lilley, et al.³⁸. According to Lilley, et al.³⁴, degrowth and growth experiments were carried out in a room maintained at 18 °C. Regarding food concentration, no prey was used in degrowth experiments whereas jellyfish were fed ad libitum during growth measurements. Facing important uncertainties that represent the term “ad libitum”, a food concentration vector specific to laboratory condition was tested with the SMCE approach (F_lab, see Table 1).

An annual climatology based on weekly measurements of sea surface temperature and zooplankton concentrations, recorded from plankton imaging, were calculated for the 2011–2015 period. Zooplankton biomass was estimated in carbon units by converting zooplankton biovolume to biomass following the linear model of Alcaraz, et al.⁶⁸, which was developed for the northwestern Mediterranean Sea. As previously mentioned, P. noctiluca undergoes nycthemeral migrations from the surface towards the bathypelagic⁶⁹. This behavior was integrated by calculating ecophysiological rates for both sea surface temperature and bathypelagic temperature (i.e., 13 °C in the Mediterranean Sea). Then, the average of each ecophysiological rate at time t was computed to represent the average daily rates.

SMCE processing

We ran 500 simulations for each parameter set which gave a 5% estimation precision and an error rate of 1% on the probability that the parameter set is correct (i.e., qualified as Match). The experiment was performed on a 64 cores CPU, 512 Go Ram, 13 To HDD computer, and ran for 8 080 minutes (i.e., 6 days). In the end, the SMCE returned all parameter sets that presented a Match greater than 70%. Additional characteristics were also returned, such as the average number of simulations that were found outside the confidence interval defined from data observation (Score), and the distance to the interval (Dist) together, for laboratory and in situ conditions. The ecophysiological model implementation is available at https://gitlab.univ-nantes.fr/delahaye-b/Pelagia-Noctiluca.

Abundance and biomass estimation

The Ligurian Sea is an area in the northwestern Mediterranean Sea that presents its own cyclonic circulation⁷⁰. Indeed, two different Modified Atlantic Waters (MAW) are mixed around Corsica and formed the “Northern current”. This strong flow progresses anticlockwise eastward along the Italian and French coasts. The Northern current exhibits specific physical and biological conditions and splits the basin into three different hydrographic zones: (i) the peripheral zone, (ii) the frontal zone and (iii) the offshore central zone. Our study monitored the distribution of P. noctiluca from 2012 to 2015⁷¹ with a quantitative method. Briefly, thanks to the French ship (www.alchimie-mediterranee.fr/, Alchimie), each cruise was carried out at night from Villefranche-sur-Mer (43°41′N, 7°18′E) to Calvi (42°34′N, 8°45′E). During this transect, only adult P. noctiluca were recognized and counted every 10 minutes. The jellyfish biomass was estimated thanks to the wet mass from sampled adult individuals.

Sinking and remineralization rate experiments

Adult P. noctiluca were collected at the surface with a dip net (1 mm mesh size) close to the frontal zone. Each individual jellyfish was placed in an 8 L plastic bucket filled with filtered (100 μm) in situ seawater. Few hours were necessary for the gelatinous organisms to egest their gut content in the form of digestive mucus. The excreted particulate matter was individually incubated in sealed vials of 33.4, 67.9 or 136.5 mL filled with filtered (0.2 μm) seawater to determine the remineralization rate. Each vial contained small optodes foil glued inside their glass wall⁷². Optodes excited by light pulses emit a fluorescence pulse in response that depends on the oxygen concentration of the solution (quenching). The phase delay of the light response provides oxygen saturation rates for the incubator. This system (optical electrodes Presens ©), is a non-intrusive and precise method (precision: 0.4% of O₂ air saturation) but it is sensitive to temperature and pressure. For this reason, it is necessary to calibrate each vial under controlled conditions before experimental measurements (need to re-calibrated every 2 months). In parallel, other vials were prepared without particles to obtain the control condition. Average respiration from control measurements was subtracted to experimental measurements with gelatinous mucus. All incubations (n = 33) ranged between 9–20 h. At the end of the experiment, each particle of mucus was frozen at −60 °C for CHN analysis. The degradation rate of organic matter was calculated thanks to a linear regression based on the decrease of O₂ in time. Thanks to the final amount and degradation rate, both carbon content at the initial time and remineralized can be estimated. In another way, sinking speed rate experiments were conducted in the laboratory. The mucus remineralization rate was estimated at 0.034 d⁻¹ function to the CO₂ consumption measurements (Table S1).

All other individual digestive mucus was used to estimate particles sinking speed, inspired by the previous study⁷³. One by one, each particle (n = 19) was placed in the first centimeters of a large graduated plastic bucket, which was 38 cm tall and 30 cm in diameter, full with filtered in situ seawater (0.2 μm) in order to conserve identical water density. The time taken by the particles to reach between 15 and 20 cm was used to estimate the sedimentation rate. The sinking rate of the mucus produced by P. noctiluca ranges between 384 m.d⁻¹ and 1329 m.d⁻¹ with a median equal to 751 m.d⁻¹ (Table S2). The sinking rates were positively correlated with the mucus size (r² = 0.6, p < 0.05) and showed similar properties to marine snow. Finally, based on these two estimates, a mucus sinking between 0 and 200 m is expected to lose 1% of its carbon weight.

Source: Ecology - nature.com