Accelerating invasion potential of disease vector Aedes aegypti under climate change

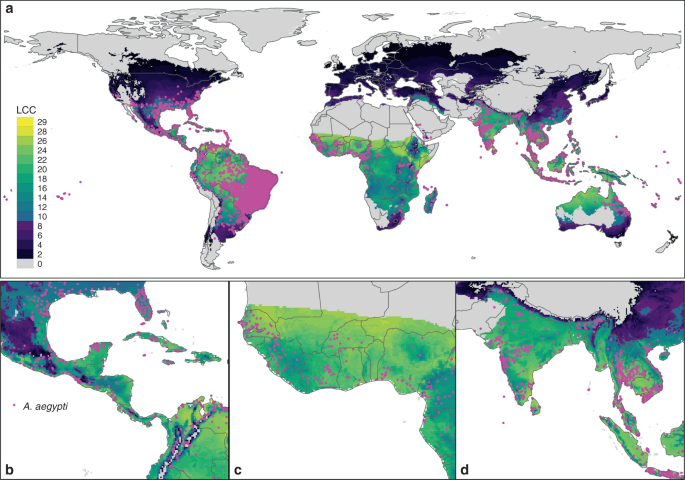
Study species

Aedes aegypti is the primary vector for several important viruses of global health concern, including dengue, zika, yellow fever and chikungunya. Previous studies have suggested that climate change may have already influenced or will influence the distribution of suitable environments in which Ae. aegypti can thrive, resulting in changes in disease risk^50,66. Beyond its health relevance, Ae. aegypti is an ideal species to use for exploring the utility of phenology models for human disease vectors because appropriate data for model parameterisation and validation are broadly available in the literature. This mosquito vector develops from the egg through a number of larval instars before emerging into adults that are only then able to transmit pathogens as the females seek blood meals to support egg development⁶⁷.

Model overview

Individual life stages and the population dynamics of Ae. aegypti are sensitive to environmental conditions, including temperature and rainfall^1,3,68, which can impact the distribution, abundance and invasion potential of the vector. In order to incorporate the environmental sensitivity of development responses of Ae. aegypti, we developed a spatially explicit phenology model incorporating each life stage of this mosquito species, following an existing phenology modelling framework²⁵. Our model calculates viability for the completion of each development stage (e.g. larvae, pupae, adult) and determines the total number of successful LCC (i.e. generations) possible per time step (e.g. month, year) given gridded climate data input. This output can be considered a development intensity index that theoretically relates to a species’ probability of occurrence, abundance and establishment potential (given successful dispersal) in specific locations. Model building and all subsequent statistical analyses were performed in R, version 3.6.1.

Model structure

The model incorporates the two main life-cycle periods of Ae. aegypti, the aquatic period (immature development) and the aerial period (adult development). The aquatic period is comprised of four stages for growth (eggs, larvae, pupae and adult emergence), while the aerial period is comprised of four adult stages (mating, blood feeding, gestating and oviposition). To simplify the life cycle, the model merges and re-divides development into four sub-stages: (1) egg hatching, (2) immature development (larvae + pupae), (3) blood feeding and (4) oviposition. These four main development stages were formulated into the model based on temperature thresholds and development rates during Ae. aegypti development (Supplementary Fig. 5). Only females were considered in the model as they are the egg producing sex. The model, similar to other studies⁶⁹, therefore assumes that there are always sufficient males to fertilize females to allow full LCC if environmental conditions allow.

The model comprises two distinct components, GDD (growing degree days) and thresholds, which together determine if and when the development of each life stage (see Rectangles in Supplementary Fig. 5) starts and completes according to prevailing environmental conditions (see diamonds in Supplementary Fig. 5). Thresholds define upper or lower limit conditions that must be met in order for the model to progress or otherwise stop. In contrast, GDD refers to the accumulation of daily mean temperature values over a baseline temperature and below a cut-off temperature beyond which there is no additional benefit^70,71. GDD calculations include a temperature threshold to mark the point at which development can occur, but thresholds are also applied elsewhere in the model on their own (e.g. heat kill, cold kill, see below). GDD is calculated based on temperature input using the formula

(T_i = 35,,mathrm{when},mathrm{above},35,)

(mathrm{GDD} = 0,,mathrm{when},mathrm{below},0,)

where i is the number of days at a particular life stage, T is the daily average temperature of the ith day since the start of the life stage (capped at 35 °C), and thr is the lower temperature threshold of development. On any given day, if T_i < T_thr then T_i − T_thr is set =0 to reflect that the accumulation of GDD cannot be negative. In components of the model that utilise GDD, if the calculated degree day (from the input climate data) is larger than the established degree day required for development/life-stage completion (derived from the literature), then development is successful and the model moves on to the next life stage. Where this condition is not met, the model cannot progress to complete a full life cycle and this failure is recorded. Conditions derived from the literature used to parameterize this component of the model for each life stage are presented below (each stage numbered in Supplementary Fig. 5):

1. (1)

   Egg hatching: A temperature-dependent egg hatching time was set considering the lower temperature threshold (baseline temperature) and GDD. Based on estimates from the literature, if the minimum temperature of the day is ≥14.59 °C and GDD since oviposition is 42.4, then the egg hatches^31,32,67. The hatch time–temperature relationship consists of faster hatching times during warmer temperatures.

2. (2)

   Immature development (larvae, pupae): After completion of the egg hatching condition, the larvae must undergo a specific amount of GDD in order to complete the aquatic immature stage and emerge as an adult. We set the baseline temperature as 11.78 °C and 126.38 GDD⁶⁷.

3. (3)

   Blood feeding: The pre-blood meal period is the time from adult emergence until the first blood meal. This period is temperature sensitive and can be as short as 1 day. It was conditioned as follows: at <20 °C, 4 days; at >20 °C, 2 days; at >26 °C, 1 day, at >35 °C, 2 days (adapted from ref. ⁶⁷).

4. (4)

   Oviposition: After feeding on the first blood meal, the adult undergoes a temperature-sensitive gonotrophic cycle (GC) to gestate and lay eggs. This period is temperature sensitive and can be as short as 2 days. It was conditioned as follows: at <26 °C, 8 days; at >26 °C, 3 days; at >30 °C, 2 days, at >35 °C, 4 days^52,56.

At the oviposition stage we also imposed a cold-kill condition, considering winter temperature is a key limiting factor for Ae. aegypti eggs to persist in the environment^56,72. To mark the beginning of a period of unsuitably cold temperatures, a condition is imposed on both temperature and duration of the cold period. If the average daily temperature is lower than the set ‘cold-kill’ temperature threshold for a specific number of days, then the egg dies and cannot proceed with the life cycle. The baseline model was set with the condition of <0 °C for 152 days, based on general consensus from the literature^56,72,73.

In addition to the model stages considered, we imposed a heat-kill condition that applied to all stages outlined above. We set an upper temperature threshold, above which development at any stage (e.g. immature and oviposition) fails to progress. Data from the literature^{31,32,74,75,76} for the upper temperature thresholds for egg hatching and larval development are ≥36 and ≥36.5 °C, respectively. The heat-kill condition for the adult lifespan is >37 °C³¹. Therefore, we set the overall heat-kill condition to any daily temperature above 38 °C for 1 day, applied at any life stage.

In addition to the temperature-dependent parameters, we included a precipitation constraint. After the temperature-sensitive conditions are met, the model imposes a precipitation constraint that removes areas considered too dry to support this species. Based on the Köppen–Geiger climate classification⁷⁷ for dry regions and the literature^78,79, the precipitation threshold was set to less than 200 mm of annual rainfall, which contains 99% of observation records. We also examined the model outputs with 900 mm rainfall (95% observation records) as a sensitivity analysis (see Supplementary Table 4), which indicates the general trends are maintained with the higher threshold.

Sensitivity analyses

Given that each of our parameters are derived by integrating values from the literature, which contain inherent uncertainties related to, for example, mosquito strain, different methodologies and so on, we conducted sensitivity analyses to explore the effects of using higher or lower values for each parameter (see Supplementary Fig. 6a–c for oviposition, heat-kill, cold-kill analyses, and Supplementary Table 4 for varying the rainfall threshold analysis).

Climate data

Gridded climate data were obtained from the NASA Earth Exchange Global Daily Downscaled Projections (NEX-GDDP) dataset⁸⁰. This database provides daily minimum and maximum near-surface air temperature and precipitation from 1950 through 2100 with a spatial resolution of 0.25°, corresponding to about 30 × 30 km grid cells at the equator. Its daily temporal resolution matches the resolution at which mosquitos develop according to prevailing conditions, and for its global coverage, relatively high spatial resolution and bias-corrected climate change projections⁸¹. NEX-GDDP utilises the Coupled Model Intercomparison Project Phase 5 (CMIP5) GCMs and provides projections for two of four greenhouse gas emissions scenarios corresponding to two levels of radiative forcing (W/m²) by 2100, RCPs 4.5 and 8.5^82,83. RCP 4.5 represents a middle-of-the-road ‘stabilization’ scenario by 2100 and corresponding mean global warming of around 2.4 °C, while RCP 8.5 represents a ‘business-as-usual’ scenario with rising emissions, no stabilization and corresponding warming of around 4.9 °C by 2100³³. We took an ensemble/consensus approach^32,38,82,83, averaging outputs from four commonly used GCMs for each RCP scenario to capture inter-model variability^32,38: the Beijing Climate Center Climate System Model, China (BCC-CSM1.1); the National Institute for Environmental Studies Climate Model, Japan (MIROC-ESM-CHEM); the Institut Pierre-Simon Laplace Climate Model, France (IPSL-CM5A-LR) and the National Center for Atmospheric Research’s Community Climate System Model, United States (CCSM 4). We chose these GCMs to cover both ‘warm’ and ‘cold’ models, which are available from the NEX-GDDP. Equilibrium climate sensitivity (ECS) is at the highest in the MIROC-ESM (ECS 4.7) among all 21 GCMs from CMIP5, while it is among the lowest in BCC1-CSM1.1 (ECS 2.8) and CCSM 4 (ECS 2.9). IPSL-CM5A-LR provides an intermediate (ECS 4.1). An alternative high quality gridded climate dataset, the ECMWF ERA5 hourly climate data, is available and more directly based on observation records; however, at the timing of writing it only covers the period from 1979 to 2019 and use of inconsistent datasets for historical and future climates makes comparisons between these two periods difficult. As such, we present results from the NASA NEX-GDDP data (1950–2050) but provide sensitivity analyses (long-term trends and spatial averages) to compare the two gridded climate datasets for the period 1980–2005 (see Supplementary Figs. 7 and 8).

Model validation

We assumed that LCC is a minimum requirement for establishment and hence occurrence, and that a greater number of LCC should correlate with both higher probability of occurrence and greater abundance. Before applying the model, the ability for the model to predict locations where Ae. aegypti can theoretically complete full life cycles was therefore validated using (1) existing Ae. aegypti occurrence records and (2) regional-scale abundance data.

The model output (i.e. LCC) was first evaluated against occurrence records of Ae. aegypti⁸⁴, which includes a global geographic dataset of occurrence records for Ae. aegypti derived from both published and unpublished sources, including national entomology surveys and expert communications. This is currently the largest available standardised global dataset for Ae. aegypti, with about 40,000 georeferenced observations⁸⁴. The predicted LCC results averaged over the years 2001–2010 were compared with known observation records of Ae. aegypti restricted to the same period and summary statistics computed. AUC was examined for the model’s ability to discriminate areas of occurrences from areas where it has not been observed based on the observation of other mosquito species as pseudo-absence points, following the same methods as in ref. ⁴⁹. For this analysis, AUC, Kappa based on confusion matrix and Pearson correlation between observation and absence were calculated at the global-scale analysis. To calculate the AUC, the life-cycle values were first standardised on a 0–1 scale, where 1 equates the maximum number of life cycles. For Kappa, we set the LCC threshold to consider presence as 10 LCC, which we defined as invasion frontier. In addition to the global-scale validation, we also calculated country-level metrics to see if our global model can be informative at the local scale.

Second, we compared LCC predictions with Ae. aegypti abundance data from Lozano-Fuentes et al.³⁴, who conducted Ae. aegypti abundance surveys in villages distributed across a large elevational gradient (0–2000 m) in central Mexico^34,35. This study was conducted in 2011 and represents the best available case study that we are aware of focusing on Ae. aegypti abundance. The surveys spanned a relatively large geographic area (300 × 100 km) and, critically, employed the same sampling methodology across all surveys. We utilised data from all villages in the study, excluding Orizaba and its ‘dormitory’ city of Rio Blanco³⁵, leaving surveys from ten villages for analysis (see Supplementary Table 2). For the validation analysis, we extracted the average LCC of our model at the locations for these villages in the same year of the sampling effort (2011) and correlated these values against abundance estimates from the surveys (adult mosquitos). As such our comparison is relative rather than absolute.

Global spatial and temporal trends in LCC intensity

Spatially explicit historical and future projections under the two RCP scenarios (4.5, 8.5) over the 100-year period (1950–2050) were conducted to evaluate whether and where environmental suitability for the LCC of Ae. aegypti has changed through time due to recent and projected climate change. In addition to presenting the gridded global LCC output maps for comparison with Ae. aegypti occurrence records and across select time periods, we averaged LCC over a number of relevant spatial (e.g. continental, climate type, latitudinal bands; Supplementary Fig. 2) and temporal (e.g. yearly, monthly; see below) scales in order to assess overall changes of LCC intensity at these scales through time. Throughout the analysis, we used 5-year averages to define and better assess key time periods: we refer to the 1950s as the 1950–1954 average, the 2000s as the 2000–2004 average and the 2050s as the 2050–2054 average.

Invasion frontiers

Ae. aegypti has expanded its global range in recent decades, with changes in environmental suitability at invasion fronts likely facilitating this spread in some instances. We thus investigated how changes in predicted LCC due to climate change at three focal invasion fronts (USA, China, Europe) could contribute to expanding ranges. To do this, we defined an invasion frontier contour as a contour line representing the LCC value below which 2.5% of Ae. aegypti occurrence records globally occurred, representing uncommon but demonstrated establishment at the lower end of the LCC distribution. Globally, this 2.5% contour line corresponds with the areas ≤10 LCC per year, so this was set as the invasion frontier threshold. We then tracked this invasion frontier contour through time to illustrate which new areas could become suitable for future establishment and by when. Invasion speed was estimated by average minimum distance between sampled points on a leading edge of an invasion frontier contour of a target year (e.g. 2050) to comparative invasion frontier contour of a previous period (e.g. 2000). The number of sampled points ranged from 300–700, depending on the shape and length of an invasion frontier contour.

Seasonality of LCC intensity

In many parts of the world, mosquito population dynamics are strongly seasonal, contributing to temporal variations in risk for vector-borne diseases⁸⁵. In particular, mosquito populations may be influenced by the seasonal effects in both peak development and the overall duration of periods in which development is enhanced. To evaluate potential changes in the seasonality of development intensity for Ae. aegypti under climate change, we estimated LCC for each grid cell monthly for each year in the analysis. We summarised these results in latitudinal categories (0–10, 10–20, 20–30 and 30–40°, N and S) to facilitate interpretation. We also used seasonal Kendall trend tests and Sen slope estimation implemented with the EnvStats package in R to evaluate and compare long-term trends across periods and latitudinal bands accounting for seasonality.

Source: Ecology - nature.com