Field work
In all, >1500 environmental samples were collected from terrestrial mosses, soils (top layer, ±upper 2 cm), and littoral sediments from lakes and ponds, originating from various locations worldwide. All samples were stored dark, and if possible, cool (<10 °C) during transport. From these, P. borealis cultures were established and used for morphological and molecular analyses. For a subset, duplicate samples were taken in the field for environmental metabarcoding. These samples were stored dark, and if possible, frozen (−20 °C). When samples could not be frozen, Sucrose Lysis Buffer (SLB; 20 mM EDTA, 200 mM NaCl, 0.75 M sucrose, and 50 mM Tris-HCl at pH 9) was added to prevent biological activity, and to preserve DNA quality. Upon arrival in the lab, all samples were frozen at −80 °C, prior to DNA extraction.
Culture establishment
Upon arrival in the laboratory, small quantities of the natural material (subsamples) were incubated for several weeks to months in WC medium, without pH adjustment or vitamin addition, at 4 °C (for polar and temperate regions) or 18 °C (for subtropical regions), 5–10 µmol photons m−2 s−1 and a 12:12h (light:dark) cycle. Although the abundances of P. borealis cells were low in the overall majority of the samples, this was accommodated by careful sample treatment. All environmental samples were subsampled in multiple wells of 12-well plates. In doing so, care was taken to take material from different parts of the sample, and if the sample was heterogeneous (for example, a mix of soil and moss), multiple subsamples from these different parts were taken. These samples were subsequently screened repeatedly in a light microscope over a course of several weeks. In case only dead valves of P. borealis were observed, samples were screened over longer time periods (up to four to six months). Although time-consuming, this approach ensured that the chances of observing living P. borealis cells were maximized. Isolations of P. borealis cells were performed whenever it became possible to find living cells. Monoclonal cultures were established by isolating single cells under an Olympus SZX9 stereomicroscope using a needle and a micropipette. Cultures were grown in WC medium at standard culture conditions of 18 °C, 5–10 µmol photons m−2 s−1 and a 12:12h (light:dark) cycle, and reinoculated when reaching late exponential phase. When sufficient biomass was obtained, subsamples for morphological and molecular analysis were taken. In total, cultures were established from 207 samples (Supplementary Data 1). Previously published strains of P. borealis17,18,20 were also included in the dataset, resulting in a total of 867 cultures (Supplementary Data 2).
DNA extraction and sequencing
Two datasets were built: a haplotype dataset (for species delimitation), and a species dataset (for phylogenetic inference). For the haplotype dataset, strains were sequenced for the D1–D3 region of the nuclear-encoded large subunit (LSU) rDNA (28S), and/or the mitochondrial cox1 (Supplementary Data 2), as they have proven to be highly suitable for single-locus species delimitation in the genus Pinnularia19. Based on the results of the species delimitation on the haplotype dataset, a selection of strains was additionally sequenced for a (subset) of four additional genes to generate the species dataset: the V4–V9 region of the nuclear-encoded small subunit (SSU) rDNA (18S), and the plastid genes psbA, psbC and rbcL (Supplementary Data 2). These genes are insufficiently variable for species delimitation in Pinnularia19, but sufficiently variable for phylogenetic inference in diatoms13.
DNA extraction was performed following a bead-beating method with phenol extraction and ethanol precipitation46. PCR reaction mixtures for 18S, 28S (primers PBLSU1F, 1R, 2F, 2R), cox1, psbA and psbC contained per sample 1 µL of the template DNA, 0.5 µM of each primer, 200 µM of each deoxynucleoside triphosphate (dNTP), 0.4 µg µL−1 of bovine serum albumin (BSA), 2.5 µL of 10x PCR buffer (Tris-HCl, (NH4)2SO4, KCl, 15 mM MgCl2, pH 8.7 at 20 °C; ‘Buffer I’, Applied Biosystems, Foster City, California USA) and 1.25U of Taq polymerase (AmpliTaq, Perkin-Elmer, Wellesley, Massachusetts USA). The mixtures were adjusted to a final volume of 25 µL with high performance liquid chromatography (HPLC) water (Sigma, St. Louis, Missouri USA). For 28S (primers DIR-f and T24U) and rbcL, 0.4 µM of each primer was used. The PCR-primer, protocols and references are listed in Supplementary Table 1a, b. In case standard PCRs failed, nested PCRs were used to obtain 28S- and cox1-sequences, using the same PCR settings as outlined above. Nested PCRs for 28S involved the external primers T24U and DIR-f, combined with the internal primer sets PBLSU1F/1R or PBLSU2F/2R, respectively, and PBORcox1F/1R (external) combined with PBORcox2F/2R (internal) for cox1. The PCR products were sequenced with their respective PCR primers and additional sequencing primers (Supplementary Table 1a). PCR products were sent for sequencing to Macrogen (http://www.macrogen.com). The obtained chromatograms were individually edited using BioNumerics v3.5 (Applied Maths, Kortrijk, Belgium).
Preparation of the datasets
Sequences were aligned using CLUSTAL-W as implemented in BioEdit v7.2.547, and subsequently manually curated. All protein coding gene sequences aligned unambiguously without any gaps. Prior to all downstream analyses, the best-fit models for nucleotide substitution were calculated (Supplementary Table 3). For the single-gene alignment of 28S the Bayesian Information Criterion (BIC) in jModelTest v2.1.348 was used. For the single-gene alignment of cox1 as well all multi-gene alignments, PartitionFinder v1.1.049 under BIC and a greedy search algorithm was used to simultaneously assess the best-fit model for nucleotide substitution and the appropriate partition scheme. Partition testing was used to account for heterogeneity in substitution rates between and within genes, i.e. codon positions. For the six-marker dataset, a set of fourteen a priori defined partition schemes were given as input, i.e. 18S, 28S and full codon partition for all coding genes. All downstream analyses in this study were run locally, on the CIPRES Science Gateway50, or on the IQ-TREE webserver51.
Automated molecular species delimitation
Five approaches to species delimitation were applied to the two single-gene datasets of 28S and cox1: Statistical Parsimony Network Analysis (SPNA)52, Automated Barcode Gap Discovery (ABGD)53, the single threshold Generalized Mixed Yule Coalescent approach (sGMYC)54, and the Poisson Tree Processes using both the maximum likelihood (PTP) and bayesian (bPTP) implementation55. These methods incorporate both distance-based approaches (SPNA, ABGD) as well as tree-based applications (sGMYC and (b)PTP). For all analyses, the full alignments of 28S and cox1 were reduced to their unique haplotypes, resulting in 279 and 244 sequences, respectively.
SPNA was performed in TCS1.2156 using a 95% threshold as connection limit and with gaps treated as missing data. ABGD was performed on the online webserver (http://wwwabi.snv.jussieu.fr/public/abgd/). For both 28S and cox1, default settings were used, except for the distance model and the number of steps, which were adjusted to K80 and 100, respectively. The X-value was adjusted depending on the dataset (1 for 28S, 1.5 for cox1). ABGD generates a series of species hypotheses (partitions). For the cox1-dataset, the initial partition was chosen, because it retrieved almost identical results as all recursive partitions, which seemed to oversplit slightly. For the 28S-dataset, ABGD had difficulty finding a stable partition. Since the initial partition was overly conservative compared to the other automated molecular species delimitation methods, the first recursive partition was preferred, as this was the most stable partition over different prior intraspecific divergence estimates. For the sGMYC analyses, ultrametric single-gene trees were obtained in MrBayes57, using a strict molecular clock model, a GTR + I + G substitution model and full codon partitioning. Two runs of four (three heated and one cold) Metropolis-coupled Monte-Carlo Markov Chains (MCMC) were completed for 10 million generations and sampled every 1000th generation. Convergence and stationarity of the log-likelihood and parameter values were assessed using Tracer v1.658. sGMYC was performed on the 28S and cox1 consensus trees using the R-package SPLITS59. For the (b)PTP analysis, a maximum likelihood (ML) phylogeny was reconstructed for both the 28S and cox1 haplotype datasets using RAxML v8.2.460 under the same substitution models and partition schemes as for the phylogenies of the sGMYC analyses, and using 10 independent runs and 1000 pseudoreplicates. The resulting consensus tree was used as input for the (b)PTP analyses on the PTP webserver (https://species.h-its.org/ptp/). The (b)PTP analyses were run for 500,000 generations using a burnin of 25%. The trace plots were visually checked for convergence. For both genes, outgroup sequences were included in the phylogenetic analysis to allow for a correct root, but outgroup sequences were removed from the (b)PTP analyses to avoid bias due to inclusion of highly divergent sequences (following ref. 55). Adopting a conservative approach, lineages were only accepted when delineated by at least four out of five methods, for each gene separately. The results of both genes were then compared to obtain a consensus species delimitation.
As the single gene-trees of the 28S- and cox1-haplotype datasets did not show hard conflicts, both datasets were concatenated, containing all unique sequence combinations of both genes. This resulted in a total of 347 strains (28S: 345, cox1: 325). Maximum likelihood (ML) trees were obtained in IQ-TREE v1.6.761. Hundred ML optimizations and 1000 UltraFast bootstrap approximations were run using the edge-proportional model (-spp option), applying the appropriate substitution models and partition schemes as determined by PartitionFinder. All other options were left as default. Bayesian analysis (BI) was performed in BEAST v2.5.062 using a relaxed lognormal clock model, a Yule tree prior, and the same substitution models as the IQ-TREE analysis. Three independent runs were run for 150 million generations, sampling every 1000th generation. All runs were checked for convergence and stationarity in Tracer. Subsequently, the runs were combined, discarding 10% of the generations as burnin, all post-burnin trees were combined, and a maximum clade credibility tree with mean node heights was calculated.
Rarefaction and extrapolation
Individual- and sample-based interpolation (rarefaction) and extrapolation was performed in EstimateS63. The analyses were run separately for the results of the species delimitation of 28S and cox1. For all analyses, 100 randomizations were run and rarefaction curves were extrapolated until a total of 4000 individuals or samples was reached.
Phylogenetic analyses
For each species identified by the automated molecular species delimitation methods, one strain was selected for downstream analyses. ML single gene trees of all six genes (cox1, 18S, 28S, psbA, psbC, rbcL—Supplementary Table 1c) were obtained in IQ-TREE using 100 ML optimizations, 1000 standard non-parametric bootstraps (-b option) and the appropriate substitution model as estimated in jModelTest/PartitionFinder. All other options were left as default. Since the single-gene trees did not show hard conflicts, all six genes were concatenated to estimate the species tree, using the appropriate substitution models and partition schemes as determined by PartitionFinder. ML trees were obtained in IQ-TREE and RAxML. For RAxML, 10 independent runs and 1000 pseudoreplicates were used. For IQ-TREE, 100 ML optimizations under the edge-proportional model were run. IQ-TREE was run twice: once with 1000 UltraFast bootstrap approximations, and once with 1000 standard non-parametric bootstraps. All other options were left as default. BI was performed in BEAST v2.5.0 using a relaxed lognormal clock model, and a Yule tree prior. Three independent runs were run for 100 million generations, sampling every 1000th generation. All runs were checked for convergence and stationarity in Tracer with 25% of the generations discarded as burnin. All post-burnin trees were combined and a maximum clade credibility tree with mean node heights was calculated.
Molecular time-calibration
A time-calibrated phylogeny of the P. borealis complex was calculated in BEAST v1.10.464. In order to provide a robust framework for the time-calibration, the six-marker dataset of P. borealis was integrated into the large Pinnularia tree of ref. 65 (Supplementary Table 2). Previously published Pinnularia strains65 were resequenced to include the D3 region of 28S in the alignment, and the entire alignment was re-aligned using the methods outlined above. Four independent MCMC runs were implemented for 78–150 million generations and sampled every 1000th generation, using an uncorrelated relaxed lognormal clock model, Yule tree prior, and the appropriate substitution models and partition schemes as determined by PartitionFinder. Convergence and stationarity of all runs was checked in Tracer, after which 60% of the generations were discarded as burnin. All post-burnin trees were combined and a maximum clade credibility tree with mean node heights was calculated. For the time-calibrated Pinnularia phylogeny, four calibration points were used using uniform prior distributions to account for the fragmentary nature of the fossil record of freshwater diatoms (Supplementary Fig. 6). The calibration strategy was based on ref. 65, updated to include newly available data and fossils (Supplementary Fig. 6b, c). The stem node of P. borealis was constrained based on the recovery of P. borealis fossils from Continental Antarctica (Supplementary Fig. 6b).
Diversification analysis
Lineage-through-time (LTT) plots were obtained using Phytools66 in R (function ltt95). The analysis was run on a subset of 1000 randomly sampled post-burnin trees from the BEAST time-calibrated analysis, which allowed obtaining a 95% confidence interval. Prior to the analysis, the BEAST trees were pruned to only contain specimens from the P. borealis complex.
Net diversification rates were calculated using the bd.ms function in the R-package Geiger67, based on ref. 26. This function requires an extinction rate as input. Since no information is available on extinction rates in the P. borealis complex, we used the diatom-wide relative extinction rate obtained by ref. 13 as input: 0.751 lineage−1 Myr−1. The bd.ms function also requires an estimate of the total number of species within the dataset. Based on the extrapolation of the rarefaction curves, the average number of sampled species was estimated on 30.36%. This is likely still an underestimating on a global scale, resulting from the lack of data from large geographic areas. We therefore also ran bd.ms with a sampling coverage of 10%. Finally, we considered a complete sampling coverage to provide an absolute baseline for P. borealis diversification.
Changes in diversification rates through time were investigated using four different models: (i) the Compound poisson process on Mass Extinction Times (CoMET) analysis68 in TESS28, (ii) the Bayesian Analysis of Macroevolutionary Mixtures (BAMM)27, (iii) the Missing State Speciation and Extinction model (MiSSE)29, and (iv) the Cladogenetic Diversification rate Shift model (ClaDS)30. The analyses were run on the time-calibrated molecular phylogeny (maximum clade credibility tree) of the P. borealis complex, after pruning the outgroup specimens, and using the same sampling fractions as outlined above.
The CoMET analysis was run in TESS v2.1.028. Empirical hyper-priors for the analyses were based on the default settings in the TESS manual, with exception of the number of expected mass extinction events (λM) and the number of expected rate changes (λB), which were both set to one. Although CoMET analyses are relatively robust to the choices of the hyper-priors, the analysis with a 30% sampling fraction was rerun using an λB of two to test for robustness of the results, revealing no difference in the outcome of the analysis. The analyses were run for a maximum of 10 million reversible-jump MCMC iterations, and assuming a uniform sampling strategy.
For the BAMM v2.5.027 analysis, the expected number of shifts equaled one, and the starting values for the priors were estimated using the setBAMMpriors function in BAMMtools v2.1.627. Four independent MCMC chains were run for 10 million generations, sampling every 1000th generation. The analyses were checked for convergence (ESS > 200), discarding 10% as burnin, and were visualized using BAMMtools.
The MiSSE model was run using the R-package hisse29. For each sampling fraction, four analyses were run, using one to four hidden states for the turnover fraction. The extinction fraction was not varied. All other settings were kept default. The AIC (Akaike Information Criterion) values of these models differed only with a couple of units. Therefore, the results of the four models were averaged per sampling fraction to obtain a more robust estimation of diversification rates.
At last, ClaDS is able to detect small rate shifts across a phylogenetic tree30. ClaDS allows to run several models, assuming extinction rates that are negligible (ClaDS0), homogeneous across all lineages (ClaDS1), or varying across lineages, but with a constant turnover (ClaDS2). We initially ran ClaDS2 using the R-package RPANDA69 for all three sampling fractions for 500,000 generations using three chains (~3 weeks run time per analysis), after which all analyses were still far from converged. These computational limitations and convergence problems when extinction is taken into account and/or missing taxa are present in the tree are well-described in the ClaDS paper30. Therefore, we limited the analysis to a ClaDS0 run assuming a 100% sampling fraction. The results of ClaDS thus have to be seen as an illustration of the prevalence of small rate shifts throughout the history of P. borealis, rather than absolute values of P. borealis diversification. We ran ClaDS0 initially for 2,000,000 iterations, thinning every 200,000 iterations and using three chains. Subsequently, the gelman statistic was calculated and additional rounds of 2,000,000 iterations were added until the gelman factor was below 1.05. Following visual inspection of the MCMC chains, the first 900 recorded chain states were discarded, after which the posterior maximas of the rates were calculated. Finally, it is worth noting that at the time of publication of this manuscript, a new version of ClaDS had become available that allows for data augmentation, and promises to substantially speed-up analyses of large datasets with missing data under the ClaDS2 model.
Historical biogeography and ancestral habitat reconstruction
The historical biogeography of the P. borealis complex was investigated in BioGeoBEARS37. BioGeoBEARS combines a ML implementation of the three most commonly used models in historical biogeography and thus allows choosing the most optimal model for a given dataset: (i) the Dispersal-Extinction Cladogenesis Model (DEC), (ii) Dispersal-Variance Analysis (DIVALIKE), and (iii) the BayArea model (BAYAREALIKE) (see ref. 37 for details). For all three implementations, BioGeoBEARS additionally allows the specification of founder-event speciation (+j)37. It is worth noting that critiques have been raised on the use of the founder-event parameter j in DEC models70, although others have argued that the latter study shows several fundamental flaws71.
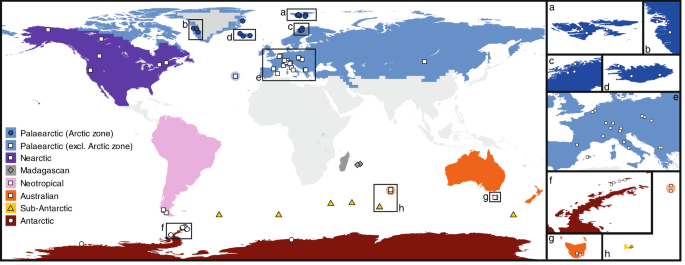
As input, BioGeoBEARS requires a time-calibrated molecular phylogeny, a set of geographical areas, and a maximum number of areas that a single species can occupy. However, increasing the number of geographic areas also increases the number of potential states (i.e. possible geographic ranges that can be occupied by a species), eventually to such an extent that an analysis cannot finish in a reasonable amount of time, or does not finish at all. Therefore, we limited our analysis to eight geographical areas following ref. 72 (Fig. 1), and allowed one species to occupy maximum six geographic areas. The latter number was based on the geographic distribution of the most widely distributed species in this study (reference strain JRI15_10_06). The geographical distributions of the species were based on the entire dataset of 867 specimens as well as the metabarcoding dataset. All six models in BioGeoBEARS (DEC(+j), DIVALIKE(+j), BAYAREALIKE(+j)) were run with and without considering geographic distance, resulting in twelve runs. All models contained parameters d (rate of range expansion) and e (rate of range contraction). In addition, the distance model contained a distance-based dispersal model (+x)73. This model estimates dispersal probability as a function of distance, and requires a distance-matrix as input (Supplementary Fig. 9). The geographic distances in this matrix were obtained by calculating the minimal great-circle distance between the two closest sampling points from each pair of geographic areas as defined above. In order to avoid problems with ML optimizations, all distances were rescaled to values between zero and one, by dividing each distance by the largest distance in the matrix. The best-fit model was selected using AIC values, and the resulting ancestral state probabilities for each node were plotted on the time-calibrated phylogeny of P. borealis. Biogeographical Stochastic Mapping (BSM)74 under the best-fit model allowed assessing the probabilities of different speciation events at each node in the phylogeny.
An ancestral habitat reconstruction was performed in Mesquite v3.6175 by means of ML reconstruction using the Mk1 model. As input, the time-calibrated phylogeny of P. borealis, including the Pinnularia outgroup, was used. Three habitat types were taken into account: aquatic (submerged environments), terrestrial and shared.
Phylogeography
Distinct sequence clusters could be observed within the lineage with the highest amount of sequence data and the widest geographic distribution (reference strain JRI15_10_06, clade 1). AMOVA39 was used to test whether this sequence variation was geographically structured between the Northern and the Southern Hemisphere. Since cox1 showed distinctly more sequence variation than 28S, only the former was used for the AMOVA test. Prior to the analysis, the alignment was reduced in order to include a maximum number of sequences and variable positions, resulting in 68 cox1 sequences belonging to 17 haplotypes. Following this reduction, all strains from some regions were removed from the dataset, but a sufficient number of strains from both hemispheres were retained to rigorously test for between-hemisphere population differentiation. AMOVA was run using the amova function of the R package ade476 and using the original, as well as clone-corrected data. The clone-corrected dataset included one representative genotype per population. Significance of the AMOVA tests was assessed using a randomization test (function randtest) with 999 permutations. P-values were corrected for multiple testing using Bonferroni correction. Haplotype networks were visualized using TCS as implemented in PopArt v1.777.
Molecular time-calibration was used to estimate the ages of the different sequence clusters. A subset of the 28S–cox1 haplotype alignment was obtained, covering four closely related lineages (reference strains JRI15_10_06, (Sterre6)c, MAQ17_160b_03, and JRI15_18b_09) and 48 specimens. rbcL was added for those strains for which it was available. The dataset was calibrated in time using BEAST v1.10.4 using an uncorrelated relaxed lognormal clock model, a coalescent constant population size tree prior, and three calibration points with uniform prior distributions (Supplementary Fig. 13). The minimum – maximum boundaries of these calibration points were based on the 95% HSP intervals of the corresponding nodes in the time-calibrated phylogeny of P. borealis (Supplementary Fig. 6). Three independent runs of MCMC iterations were implemented for 5 million generations and sampled every 1000th generation. Convergence and stationarity of the runs was checked in Tracer, after which 10% of the generations were discarded as burnin, all post-burnin trees were combined, and a maximum clade credibility tree with mean node heights was calculated.
Environmental metabarcoding
A subset of 132 environmental samples in which P. borealis was detected by light microscopy or by a previous yet unpublished metabarcoding analysis performed in our lab (PAE, Ghent University) was selected for environmental metabarcoding (Supplementary Data 3). The environmental samples (on average 5 g wet material/sample) were purified by coagulating and removing the extracellular DNA and proteins following ref. 78, after which the DNA was extracted using the protocol by ref. 46. The V4-region of 18S was amplified using the universal primers TAReuk454FWD1 and TAReukREV310679. PCR amplifications were performed in duplicate to reduce stochastic effects. The PCR mixtures contained per sample 1 µL of the template DNA, 0.4 µM of each primer, 200 µM of each deoxynucleotide triphosphate, 2.5 µL of 10x PCR buffer, and 0.25U of Fast Start High fidelity Taq polymerase (Roche Inc.). The final reaction volume was adjusted to 25 µL using HPLC water. The PCR conditions were as follows: 35–40 touch-down cycles (1 min at 94 °C, 1 min at 57–52 °C and 3 min at 72 °C) with an initial denaturing step of 5 min at 94 °C and a final step of 20 min at 72 °C. All final PCR products were purified with Agencourt AMPure XP beads. Quality control was performed with a Qubit (Thermo Fisher Inc.) and BioAnalyzer (Agilent Inc.), after which the duplicates were pooled. The amplicon libraries were barcoded using the NEXTERA xt DNA kit (Illumina Inc.) following to manufacturer’s instructions and purified using Agencourt AMPure XP beads. The libraries were randomly assigned to two runs, and sequenced on a 300 bp paired-end Illumina MiSeq machine at Edinburgh Genomics (http://genomics.ed.ac.uk/). The raw reads were processed into Amplicon Sequence Variants (ASVs) using the R-package DADA2 v1.6.035, for each run separately. The last 50 bp of the reverse readers were truncated, and the maximum expected error (maxEE) equaled 2. Samples were not pooled for the ASV inference step. Upon ASV inference, both runs were combined into a single dataset, and chimeric sequences were detected and removed. The taxonomic classification of the ASVs was done in Mothur80, using a bootstrap value of 80 and the PR2 database v4.8.081, updated to include all available unique 18S-haplotypes of P. borealis, as a reference. The identified ASVs were subsequently aligned to the reference sequence of their Mothur-ID to confirm the identifications. In addition, we reclassified the ASVs obtained in the global soil metabarcoding study of ref. 9 using our updated PR2 database to search for presence of P. borealis.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Source: Ecology - nature.com


