Urbanization and agricultural intensification destabilize animal communities differently than diversity loss

Community dynamics datasets

Yearly butterfly, bird, and bat abundance data were obtained across France from nationwide citizen science monitoring schemes, part of the Vigie Nature program [http://vigienature.mnhn.fr/]. The monitoring sites are different among taxa as they depend on the residency of the volunteers and monitoring protocol used (see below).

For bat communities, we used data from the French bat-monitoring program [http://www.vigienature.fr/fr/chauves-souris], a citizen-science program running since 2006⁴⁴. Briefly, volunteers record bat activity using ultrasound recorder while driving at a constant low-speed (25 ± 5 km/h) along 30 km circuits. These circuits were chosen to be close to the volunteer residency, with low-traffic roads for security and representative of the different land-cover types in the area. These circuits are divided into ten 2-km transects where bats are recorded, separated by 1-km road portions where recording is not carried out. Surveys start 30 min after sunset and last approximately 1.5 h. Weather conditions have to be suitable for the survey to be carried out: no rain, wind speed below 7 m/s, temperature above 12 °C. Bat activity is recorded through echolocation calls with ultrasound detectors connected to a digital recorder. Volunteers were trained to classify echolocation calls to the most accurate taxonomic level using Syrinx 2.6⁴⁵. Data validation was done by program coordinators at the Muséum national d’Histoire naturelle for recordings with uncertain identification. Following previous works (e.g.,⁴⁶), the abundance of each bat species in a 2-km road transect was defined as the number of bat pass per species (a bat pass corresponds to a trigger of the bat detector in time expansion). We used data from transects surveyed between June 15th and July 31st (seasonal bat activity peak) from four to 6 years between 2006 and 2012. This represented a total of 152 local bat communities, where a total of 7 species were recorded (Supplementary Table 1).

For bird communities, we used data from the French Breeding Bird Survey [http://www.vigie-plume.fr/]⁴⁷, a monitoring program relying on keen birdwatchers to count birds annually in a given plot. Plots are squares of 2 × 2 km² randomly selected by the national coordinator, within which the surveyor places 10 points separated by at least 300 m, in order to cover all the habitats present in the plot. Each plot is surveyed twice a year, the first session (to record nonmigrant birds and short distance migrants) between April 1st and May 8th, the second (to record trans-saharian migrants) between May 9th and June 30th, with at least 4 weeks between both sessions. Surveying dates must be the same (±5 days) every year, and counting takes place in the morning, starting 30 min after sunrise, with points always visited in the same order. At each point, the volunteer spends 5 min recording all birds seen or heard. Following previous work (e.g.)⁴⁷, yearly species abundance at a site was calculated as the sum of the maximum number of individuals detected per point over the two sessions. For this study, plots surveyed at least eight years between 2001 and 2017 were selected, representing 269 local bird communities and 75 common species for which the amount of data available allows an accurate estimation of population dynamic (Supplementary Table 1).

For butterflies, we used data from the French garden butterfly observatory [http://www.vigienature.fr/fr/operation-papillons]⁴⁸. Participants identify and count Lepidoptera in their own garden, from a closed list of 28 common species or species groups (27 butterflies and one common diurnal moth, Macroglossum stellatarum). Since some of the taxa targeted by this scheme group several look-alike species (species groups), we only kept the 13 butterflies and 1 moth identified at species level for our analyses (Supplementary Table 1). The temporal variability of the butterfly community restricted to these 14 species reflects that of the community including the abundance of the species groups (Supplementary Fig. 6). For each species, abundances are recorded monthly, as the maximum number of butterflies seen simultaneously during the month. Counting takes place from March to October, but for this study, gardens that had been monitored in July at least seven years between 2007 and 2018 were selected, except for the year 2014 because of a crash of the database server, representing 130 local butterfly communities.

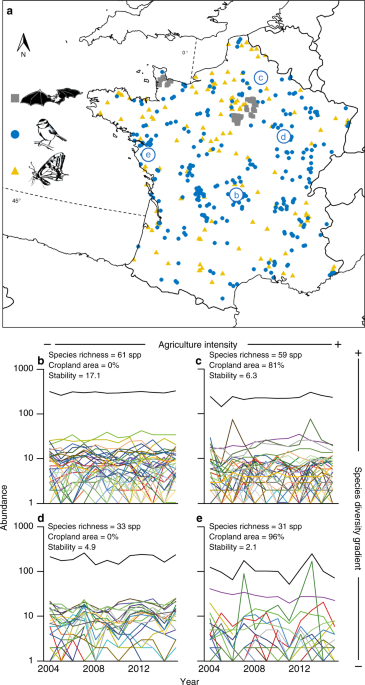
Our data selection presented and analyzed in the main text totalized 551 sites (Dataset 1), with variations in the number of years across sites and taxa. This leads to 65, 7, and 80 sites with time series of, respectively 4–6 years for bats; 3, 14, 37, 32, 29, 33, 49, 30, 30, and 12 sites with time series of, respectively, 8–17 years for birds; and 34, 12, 10, 17, and 57 sites with time series of, respectively, 7–11 years for butterflies.

To test the robustness of our results to the presence of gaps in the time series, we also ran our analyses on two subsets of the dataset that included only time series of the same duration and with no missing year. The first subset was restricted to the longest fully overlapping observation period with no gap common to all sites, leading to times series of 4, 8, and 7 years for bats, butterflies and birds, respectively (Dataset 2). The second one was restricted to sites having the longest fully overlapping observation period with no gap, leading to time series of 5, 12, and 11 years, for bats, birds, and butterflies, respectively. This last data selection procedure reduced the number of sites included to 87, 106, and 57, for bats, birds, and butterflies, respectively (Dataset 3). The analysis of the three datasets gave qualitatively similar results (Supplementary Figs. 7–9), confirming the robustness of our results to both the presence of gaps and the number of communities studied.

Community species diversity and phylogenetic diversity

For each local community, we estimated the species diversity as the exponential of the Shannon diversity index calculated from the summed yearly abundance across all years for each species seen in a site during the survey period. We assessed the phylogenetic diversity of each community using the MPD index weighted by species abundances⁴⁹. As the weighted MPD was correlated to species diversity for the three taxa, all analyses were performed using the residuals of the weighted MPD against the species diversity (Supplementary Fig. 10).

The weighted MPD calculations were based on ultrametric molecular phylogenetic trees⁵⁰. For bats we used the phylogenetic tree provided by Shi and Raboski⁵¹ (Supplementary Fig. 11). For birds we extracted 1000 trees from the phylogeny published by Jetz et al.⁵² and computed the Maximum Clade Credibility tree with branch lengths equal to the median of the branch lengths of the 1000 trees using TreeAnnotator 1.7.5⁵³ and without burnin. The resulting tree was well supported, with 93% of the nodes having a Bayesian Posterior Probability > 0.9 (Supplementary Fig. 12). For butterflies, we downloaded published sequences for the following genes: cytochrome oxidase c subunit 1 (COI, 657 bp), elongation factor 1 alpha (EF1α, 1239 bp), glyceraldehyde 3-phosphate dehydrogenase (GAPDH, 690 bp), ribosomal protein S5 (RPS5, 616 bp), wingless (wg, 402 bp) (Supplementary Table 4). Sequences were aligned using CodonCode Aligner 6.0.2 [http://www.codoncode.com], and the different genes were concatenated. Phylogenetic analyses were performed in a Bayesian framework using BEAST 1.8.1. The dataset was partitioned by gene. Unlinked GTR + Γ model of nucleotide substitution and uncorrelated lognormal clocks were implemented for all partitions. The MCMC analysis was run for 100 million generations, and sampled every 100,000 generation, which resulted in 1000 trees. After checking for convergence, we applied a 10% burnin and extracted the Maximum Clade Credibility tree with branch lengths equal to the median of those of all trees using Tree Annotator 1.7.5⁵³. Because in preliminary runs Papilionoideae monophyly was not recovered (basal relationships were poorly resolved), we enforced monophyly for this group. The MCC tree where Papilionoideae monophyly was enforced was well resolved, with all Bayesian posterior probabilities > 0.99 (Supplementary Fig. 13).

To assess the robustness of our results to the use of diversity metrics weighted by species abundances we also calculated the species richness as the total number of species seen during the survey period, and the corresponding Chao index⁵⁴ to account for imperfect detections (Supplementary Fig. 14) with R package “vegan”⁵⁵. Similarly, we calculated the MPD not accounting for species abundances. For similar reason as for the weighted diversity metric, analysis were performed with the residuals of MPD against species richness or Chao index. The use of either species richness estimates coupled with unweighted MPD residuals did not change qualitatively the results from the ones obtained using the Shannon diversity index and the residual weighted MPD (Supplementary Figs. 7–9). We present in the main text the analysis using the diversity metrics weighted by species abundances.

Temporal stability and asynchrony measures

To investigate the mechanisms by which habitat degradation and community diversity might affect the stability of local communities, we calculated the temporal stability of each of these communities as the inverse of the coefficient of variation of the community abundance across time. The temporal stability of a community abundance decreases when the coefficient of variation of the community abundance increases. To quantify the respective contribution of population asynchrony and stability to community stability, we followed Thibaut and Connolly²² and partitioned the coefficient of variation of community abundance CV into the product of an index of population synchrony (varphi) developed by Loreau and de Mazancourt⁵⁶ and the mean coefficient of variation of the population abundance (mean population variability) weighted by their relative abundances (overline {{mathrm{CV}}_w}) as:

with

and

With σ² representing the variance of the abundance of the community, σ_i the standard deviation of the abundance of the population i in the community, µ the temporal mean of the abundance of the community, µ_i the temporal mean of the abundance of the population i and CV_i the coefficient of variation of the abundance of population i. The population synchrony index (varphi) ranges from 0 (maximum asynchrony) to 1 (maximum synchrony). To get an asynchrony index that increases with population asynchrony, and population and community indices that increase with population and community stability, respectively, we used the inverses of the synchrony index and of the weighted mean coefficient of variation of population abundance. To achieve normality, we log-transformed the coefficient of variation of community, the coefficient of variation of population and the synchrony index for the three taxa.

We always have

where

Assessing habitat degradation

To characterize and quantify habitat degradation levels around the monitoring sites, we first used Corine Land Cover [https://www.data.gouv.fr/fr/datasets/corine-land-cover-occupation-des-sols-en-france/] to quantify the percentages of cover occupied by five land-use categories within buffers surrounding the study sites: urban, cropland, heterogeneous agriculture, woodland and seminatural open areas (Supplementary Table 5). To calculate the percentage of cover associated to each of our landscape variables around each study site, we used 3 buffer sizes per taxa: buffers of radius 250, 500, and 1000 m around the transect for bat and around the garden for butterfly communities, and squares of 2, 2.5, and 3 km of side for bird communities. These differences in size and shape among taxa accommodate for the shape of the sampled area and the scale at which landscape is known to affect those taxa^44,57,58. The use of either of the three buffer sizes in our statistical analyses (see below) did not change qualitatively our results (Supplementary Figs. 7–9).

Second, to account for landscape complexity, we calculated a Shannon diversity index on the area of each land-use category of the level 3 of Corine land cover (Supplementary Table 5).

To account for potential changes in the landscape during the monitoring period, we averaged the percentage areas and landscape complexity described above over the years available in the Corine land cover database that match the monitoring periods. For bird communities, we used the land cover data for the years 2000, 2006, 2012, and 2018; for bat communities, the years 2006 and 2012; and for butterfly communities, the years 2006, 2012, and 2018.

Third, to account for the intensity of both urban and agricultural land uses, we calculated two indices. The area of sealed soil from the European Soil Sealing V2 [http://www.eea.europa.eu/data-and-maps/explore-interactive-maps/european-soil-sealing-v2] (hereafter, sealed soil) that is only available for the year 2006, and an index of agricultural practice intensity (hereafter, agricultural inputs) following the European Union agri-environmental indicator of intensification-extensification [http://ec.europa.eu/eurostat/statistics-explained/index.php/Agri-environmental_indicator_-_intensification_-_extensification]. This last indicator is defined as the sum of expenses in k€ for fertilizers, pesticides, livestock food and veterinarian medics per year divided by the area of agricultural land. It was calculated for each year and administrative region using data from the Agricultural Network of Account Information (RICA) [http://agreste.agriculture.gouv.fr/enquetes/reseau-d-information-comptable/]. This indicator is available for all years except 2017 and 2018. For each site, we calculated the mean over the monitoring period.

We then performed a principal component analysis (PCA) on these eight landscape variables calculated for each monitored site, followed by a Varimax rotation⁵⁹ to ease the interpretation. The two first dimensions were used to characterize habitat degradation by an urban gradient and an agricultural intensity gradient, the two being independent from each other (Fig. 2). To achieve normality for the following analysis, we log-transformed the urban gradient for the three taxa. The PCA was performed twice, once for the Dataset 1 and 2 and once for the Dataset 3 (Supplementary Fig. 15) as the sites included differ between both.

Statistical analysis

To assess the relationship between habitat degradation gradients and community stability, we first fitted for each taxonomic group (1) a linear model with the two habitat degradation gradient as explanatory variables (Fig. 3a, b), (2) a linear model with the species diversity and the phylogenetic diversity as explanatory variables (Fig. 3c, d).

To quantify the direct and indirect effects of habitat degradation gradients on community stability, SEM was performed in the following two steps:

First, for each taxonomic group and related buffer sizes, we built a set of five linear models to assess the effects of urban and agricultural intensity gradients on species diversity (model 1) and phylogenetic diversity (model 2), the effects of urban gradient, agricultural intensity gradient, species diversity and phylogenetic diversity on population stability (model 3) and asynchrony (model 4), and the effects of the population stability and asynchrony on community stability (model 5).

Second, to disentangle direct and indirect relationships among variables, and compare the strength of significant relationships, we conducted piecewise SEM⁶⁰ for each taxonomic group and related buffer sizes. We used Shipley’s test of d-separation to assess the overall fit of the SEM⁶¹. The strength of a path from a variable on another is the product of the strength of each significant relationship along the path. The overall effect of a variable on another one is the sum of the paths joining the two variables.

For each taxon, the analysis presented in the main text correspond to that performed with the buffer size leading to the lowest AIC. All results remain qualitatively similar for all scales (Supplementary Figs. 7–9).

For all statistical analyses, spatial autocorrelation was accounted for. For bird and butterfly communities we used generalized least squares with exponential and gaussian spatial correlation structures respectively⁶². Because bat communities were aggregated in two distinct geographical regions, we used linear mixed-models with region as random effect (Ile-de-France or Manche)⁶².

To further our understanding of the effect of habitat degradation on population stability, we estimated the mean-variance scaling for each taxon by performing a linear mixed-model explaining the log of the variance of population abundances by the log of the mean population abundances, with both species and site as a random effect. We found a slope of 1.61 ± 0.029 for bats, 1.09 ± 0.004 for birds, and 1.09 ± 0.018 for butterflies, meaning that the stability of communities increases with the mean population abundance of the communities²². We verified these predictions by looking at the relationships between the weighted mean population stability and the mean population abundance for each taxon using linear models identical to those used in the path analyses (Supplementary Fig. 5). In addition, we tested whether habitat degradation gradients were correlated to either the mean population abundance of the communities or its standard deviation (Supplementary Fig. 4). Statistical analyses were performed using the R software⁶³, with libraries “PiecewiseSEM v1.2.0”⁶⁰, “nlme”⁶⁴, “picante”⁶⁵, “ape”⁶⁶, “ade4”⁶⁷, and “lmerTest”⁶⁸.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Source: Ecology - nature.com