Regime shifts occur disproportionately faster in larger ecosystems

Literature search strategy, case-study qualifications and dataset

The literature search used three electronic databases, namely the University of Southampton’s DelphiS interface, Web of Science and Google Scholar. Prospective case-studies were recognised by individual cases or combinations of the following key terms appearing within either the article title or abstract: regime shift, critical shifts, shift, abrupt shift, threshold change, tipping point, stark shift, abrupt change, human-natural system, ecosystem, ecological, social–ecological, ecosystem, irreversible, landscape, environment.

The literature search was carried out from February to August 2018. Date limits were not imposed on the year of publication. In addition, case-studies from both the Regime Shift Database⁷ of the Stockholm Resilience Centre and the Threshold Database²⁰ of the Resilience Alliance were considered for inclusion. Each potential case-study, including the social systems included in Supplementary Fig. 2, had to then meet the following three-part criteria to be included in the empirical dataset of this study:

1.
For inclusion based upon the characteristics of the regime shift, each case-study must exhibit:
1. (a)
  A demonstrated/observed state change in a real-world environment, rather than just hypothesised or modelled.
2. (b)
  Recognisable and clearly defined alternate states, consistent with common definitions, including both quantitative (e.g. ecosystem service availability) and qualitative (e.g. structural change) indicators.
3. (c)
  Driver(s) of change that are beyond natural and/seasonal variations/cycles.
4. (d)
  Irreversibility over the temporal horizon of the original study.
5. (e)
  Or, if reversed, human-led remediation efforts (e.g. artificially manipulating water quality) were completed over the course of the study.
2.
In order to confidently and consistently measure the spatial extent (and depth) of shifts, the following steps were applied:
1. (a)
  Use regime shift area (and depth where applicable) directly quoted in the case-study publication.
2. (b)
  Ascertain whether the shift occurred across the whole system or sub-system of wider geographical entity, then:
  1. i.
    Consult ‘Locational Information/Case Study/Methodology’ sections of scientific publications to find quoted area of shift.
  2. ii.
    If shift occurred across entire system, we searched within related scientific publications to find extent (and depth) of system.
  3. iii.
    Widening the search to institutional literature, such as maritime management reports.
3.
In order to confidently and consistently measure the temporal scale of shifts (i.e. the time taken to transition to a stable but functionally different system state), the literature either:
1. (a)
  Directly quoted the shift duration in text.
2. (b)
  Explicitly depicted shift duration in a time series of system conditions, with the significant deviation from the preceding regime flagged.
3. (c)
  Visually estimated shift duration from a time series of system conditions. To remain consistent, the tipping point was always identified by the first sign of significant divergence from the preceding trend.

After applying the above qualifications, the final dataset (Supplementary Table 1) includes 42 regime shifts observed in nature (25 marine, 13 freshwater and 4 terrestrial).

Sensitivity analysis of empirical results

The empirical dataset suggests that there is an overarching positive association between system area and shift duration, and that larger systems tend to shift comparatively quickly relative to their size. However, it is reasonable to ask questions around the uncertainty of this result. Therefore, we investigate the extent to which the sub-linear trend is (i) dependent on any one datapoint in the empirical dataset, and (ii) affected by uncertainties within the empirical dataset. Regarding point (i), we created 42 new empirical datasets, each with one of the empirical records removed. We fitted power-law relationships to each of the new 42 datasets (each with 41 empirical records) and assessed the degree to which removing any one empirical record impacted the production of a significant, sub-linear association between system area and shift duration. We undertook a simple Monte Carlo analysis to investigate point (ii). For each of the 42 empirical records, 5000 random error terms were generated, converting the shift durations to values between 50 and 150% of their original values. The resulting error ranges are graphically represented in Supplementary Fig. 5. Error terms were only applied to the shift durations, as confidence in the system area values is relatively high (Supplementary Table 1). From here, we fitted power-law regression models through each of the 5000 new models and recorded the resulting slope and significance coefficients. All analyses were conducted using the statistical software R⁴³.

Model selection strategy

The model search was carried out from February 2018 to February 2019, during which we identified models that reflected the characteristics of the empirical regime shifts data obtained.

1.
For inclusion based upon the characteristics of the regime shift, each model must exhibit:
1. (a)
  A state change.
2. (b)
  Recognisable and clearly defined alternate states, consistent with common definitions, including both quantitative (e.g. ecosystem service availability) and qualitative (e.g. structural change) indicators.
3. (c)
  Variables acting as driver(s) of change.

2.
In order to confidently and consistently measure the temporal scale of shifts, the model either:
1. (a)
  Explicitly depicted shift duration in a time series of system conditions, starting in an unstable state, where the start of the shift is assumed to be the start of the model run.
2. (b)
  Started in a stable state, from which shift duration could be estimated from a time series of system conditions. To remain consistent, the tipping point was always identified by the first sign of significant divergence from the preceding trend (see the ‘Identifying regime shift durations of modelled time series’ section for more details below).

3.
In order to investigate the impact of system characteristics, the model either:
1. (a)
  Allowed for variation in system size.
2. (b)
  Allowed for variation in metrics of system fluidity or connectedness.

4.
Finally, in accordance with FAIR principles⁴⁴, models were required to be open-access.

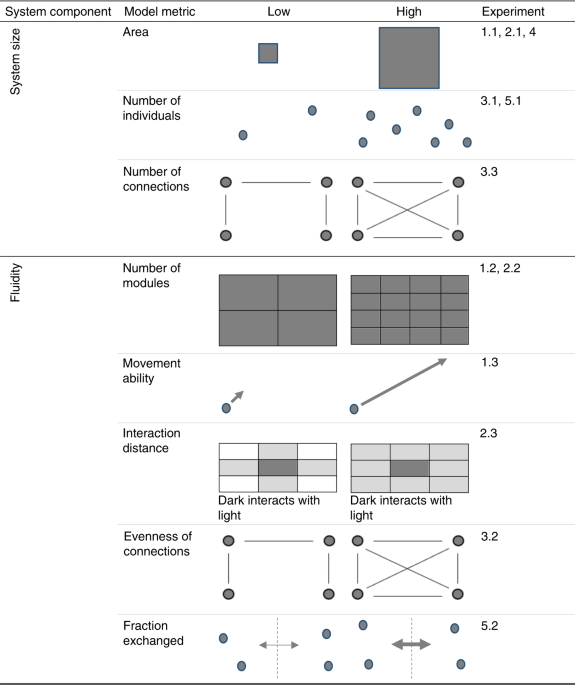
After applying the above qualifications, we obtained five models of regime shifts that are findable, accessible and reusable as well as being comparable to our empirical data. Of these models, two are known to illustrate tipping points and hysteresis (CHL and SH models). The models are described below.

The Wolf-Sheep Predation (WSP) agent-based model

The WSP model explores the stability of predator-prey relationships²¹. The construction of this model is described in two principle articles^45,46. In our investigation, we used a variation of the model which includes grass in addition to wolves and sheep. Both wolves and sheep are randomly generated and move randomly through a landscape. Each step costs both animals in terms of energy; wolves must eat sheep and sheep must eat grass in order to replenish their energy. Therefore, any animals that run out of energy die. Once grass has been eaten, it will regrow after a fixed number of model steps. Finally, every animal has a fixed probability of reproducing at each time step. This model is freely available within the NetLogo software⁴⁷ and the default values for the model variables are shown in Supplementary Table 3. The WSP model outlined above is sometimes stable²¹, but can be made unstable by varying the grass regrowth time. Once the model is unstable, it can be observed to go through three possible regime shifts (Supplementary Fig. 7): (1) the extinction of wolves, (2) the extinction of sheep, (3) the progression of the landscape to full grassland, which with no grazers present, could lead to succession towards another ecosystem state. By altering specific variables and then destabilising the WSP model we were able to investigate the impact of those variables on the duration of the regime shifts. The variables we investigated using the WSP model were system area, module size, and system fluidity (Table 1). To investigate the impact of the area of the landscape on the duration of the regime shift, we increased the length and width of the landscape by two pixels at a time between 1 and 100, while maintaining constant starting densities of both wolves and sheep (Supplementary Table 3). To ensure unstable systems, the reproduction rates of sheep were altered to a constant of 7% and grass regrowth time was varied from 1 to 100. Using the ‘BehaviorSpace’ tool within Netlogo⁴⁷ every variation of this model was run for 5000 time steps, unless all three regime shifts occurred prior to this. This process resulted in 260,100 model runs. To investigate the impact of the size of modules within the landscape on the duration of the regime shift, we varied the height of the landscape between 2, 5, 10, 20, 50, and 100 cells. Here we again maintained constant starting densities of both wolves and sheep, but summed model runs together so that world size was consistently 100 × 100 pixels (Supplementary Table 4). To ensure unstable systems, the reproduction rates of sheep were altered to a constant of 7% and grass regrowth time was varied from 1 to 100. As per the world size experiment, every variation of this model was run for 5000 time steps, unless all three regime shifts occurred prior to this. This process was repeated 100 times, resulting in 930,000 model runs. To investigate the impact of the system fluidity on the duration of the regime shift, we varied the mobility of the animals between 1 and 100, while maintaining a constant landscape size of 100 × 100 pixels (Supplementary Table 4). To ensure unstable systems, the reproduction rates of sheep were altered to a constant of 7% and grass regrowth time was varied from 1 to 100. Every variation of this model was run for 5000 time steps, unless all three regime shifts occurred prior to this. This process resulted in 10,000 model runs. The GoL model can be obtained from the following URL: https://ccl.northwestern.edu/netlogo/models/WolfSheepPredation

Game of Life (GoL) cellular automaton model

In the two-dimensional GoL each cell can be either one of two possible states: ‘alive’ or ‘dead’. At every time step, each cell checks the state of itself and its neighbours, and then sets itself as either alive or dead based on its neighbours’ states. This model is freely available within the NetLogo software²² and the default values for the model variables are shown in Table S5. The GoL model outlined above is inherently unstable when an initial density of 35% is used (i.e. the system begins to shift from the initial state to the alternative state as soon as the model run begins). Upon starting the model at this density, the number of ‘alive’ cells decreases until a stable state is reached. Thus, the system can only be observed to go through one possible regime shift: from an unstable state with both alive and dead cells to an alternate stable state in which either all cells are dead, or a stable mixed state has been reached. By altering specific variables we were able to investigate the impact of those variables on the duration of the regime shift, starting from an unstable state. The variables we investigated using the GoL were system size, module size, and system fluidity (Table 1). In order to determine when stability occurred, we inserted a new stop function (Supplementary Note 3) which would stop the model if the number of living cells did not change for 100 time steps. To investigate the impact of the size of the landscape on the duration of the regime shift, we increased the length and width of the landscape by two pixels at a time between 1 and 100, while maintaining consistent starting densities of both alive and dead cells (Supplementary Table 5). To ensure unstable systems, the initial density was set to 35%. Using the ‘BehaviorSpace’ tool within Netlogo, every variation of this model was run for 5000 time steps, unless a stable state was reached prior to this. This process resulted in 260,100 model runs. To investigate the impact of the size of modules within the landscape on the duration of the regime shift, we varied the height of the landscape between 2, 5, 10, 20, 50, and 100, again while maintaining consistent starting densities of both alive and dead cells, but summed model runs together so that word size was consistently 100 × 100 pixels (Supplementary Table 5). To ensure unstable systems the initial density was set to 35%. Every variation of this model was run for 5000 time steps, unless a stable state was reached prior to this. This process was repeated 100 times, resulting in 930,000 model runs. To investigate the impact of the system fluidity of the landscape on the duration of the regime shift, we varied the number of neighbours each cell considered between 4 (i.e. von Neumann neighbourhood³⁴) and 8 (i.e. Moore neighbourhood³⁴), while maintaining a constant landscape size of 100 × 100 pixels and a constant proportion for the decisions to ‘die’ (Supplementary Table 5). To do this, we further adapted the standard GoL code, updating the ‘to go’ function to include both possible neighbour combinations (Supplementary Note 3). To ensure unstable systems, the initial density was set to 35%. Every variation of this model was run for 5000 time steps, unless a stable state was reached prior to this. This process was repeated 100 times, resulting in 200 model runs. The GoL model can be obtained from the following URL: https://ccl.northwestern.edu/netlogo/models/Life

Language Change (LC) network model

The LC model explores how the structure of social networks can affect the course of language change^23,24 (Supplementary Fig. 8). In our investigation, we used a variation of the model (termed ‘individual’) in which individuals can only access one language at a time. Each time step, individuals choose one of their neighbours randomly and then adopt that neighbour’s language (Language 1 or Language 2). This model is freely available within the NetLogo software⁴⁷ and the default values for the model variables are shown in Supplementary Table 6. The LC model outlined above is inherently unstable. Language 1 is created as dominant and cannot be lost once adopted²³. Thus, the system can only be observed to go through one possible regime shift: from a mixed state with two languages to an alternate state whereby language 1 has become saturated in the population (Supplementary Fig. 8). By altering specific variables, we were able to investigate the impact of those variables on the duration of the regime shift, starting from an unstable state. The variables we investigated using the LC model were number of connections, number of nodes and network connection heterogeneity (Table 1). To investigate the impact of the number of connections in a network on the duration of the regime shift, we varied the number of connections between 99 and 4500 (Supplementary Table 6). In order to do this, the number of connections was added as a global variable and the code to create the network was altered to ensure the number of connections between nodes was equal to this user-defined value (Supplementary Note 4). Using the ‘BehaviorSpace’ tool within Netlogo, every variation of this model was run for 5000 time steps, unless the regime shift occurred prior to this. This process was repeated 100 times, totalling 440,200 model runs. To investigate the impact of the number of nodes in a network on the duration of the regime shift, we varied the number of nodes between 3 and 1000 (Supplementary Table 6). The number of connections was set to one but would default to the number of nodes minus one to ensure all nodes were connected. Every variation of this model was run for 5000 time steps, unless the regime shift occurred prior to this. This process was repeated 100 times, totalling 99,800 model runs. Instead of re-running the LC model to specifically investigate the impact of network connection heterogeneity on the duration of regime shifts, we maximised computational efficiency by analysing network heterogeneity in the systems used to investigate the number of connections. During the above LC model experiments, we recorded the standard deviation of the number of connections of each link; acting as an appropriate measure of the heterogeneity of the connection distributions as the underlying distribution is normal (Gaussian; Fig. S8). The LC model can be obtained from the following URL: https://ccl.northwestern.edu/netlogo/models/LanguageChange

Lake Chilika fishery (CHL) system dynamics model

The CHL model²⁵ was built to investigate the future social–ecological sustainability of the Chilika lagoon—Asia’s largest brackish water ecosystem—located in Odisha, India. Essentially, the model simulates the coupled effects of various biophysical and socioeconomic pressures on the fish stock. As a system dynamics model, the key dynamics of the social–ecological system are represented as stocks (e.g. fish population, lake water sediment and aquatic vegetation), flows (e.g. freshwater and climatic inputs, fish births and deaths) and feedbacks (e.g. fishery intensification) which all evolve over time. Each model time step equals 1 month, although outputs are generally aggregated to the annual resolution to improve visualisation. Here, simulations are run for 1524 time steps, equalling 127 years (i.e. the period from 1973–2099). In the original model²⁵, the model simulates four socioeconomic stresses on the fish population: (i) the number of fishers able to generate their livelihood from the fishery is related to a simple carrying capacity, based on the economic revenue of the fish catch, the average income of each fleet (i.e. traditional and motorised) and the minimum cost to fish; (ii) relatively affluent traditional fishers may switch from traditional wind-assisted sailing boats to relatively fish catch intensive motorboats; (iii) the number of days fished each month is proportional to the underlying density of the fish population; (iv) while the acceptance of juvenile catch increases during stock declines to compensate for lost fishing days. The original model also captures three biophysical pressures on the fish population: (i) the effect of tidal outlet sedimentation and closure on the migration of fish to and from the Bay of Bengal, with 70% of the fish stock undertaking this migration pathway each year to complete their natural breeding cycles; (ii) the effects of lake water salinity, temperature and dissolved oxygen concentration on the survival rate of juvenile fish per unit time; (iii) the growth of surface water aquatic vegetation which provides refuge from fishery activities. The model also simulates the effects of alternative governance options, including the implementation of fishing bans and the frequency of tidal outlet maintenance (i.e. removal of accumulated sediment). The model is aspatial, as per the majority of system dynamics models. However, the model does simulate the effect of lake area on the growth of aquatic vegetation and the volume of rainfall falling directly onto the lake—with subsequent impacts on the salinity of the lake water and the accumulation of lacustrine sediment (i.e. larger area leads to higher direct rainfall inputs, leading to greater flushing of sediment from the lagoon). Therefore, to model the direct association between lake area and the duration of transition, we turn off all socioeconomic pressures (i.e. set fish catch from both fleets equal to zero). In turn, we vary the parameter named ‘Chilika area km²’ between 500 km² and 10,000 km² (i.e. 50–1000% of the original lake value). The model is run for 5000 simulations in the sensitivity analysis mode, sampling a different lake area between the minimum and maximum area limits per simulation. Tidal outlet maintenance is turned off, meaning the lacustrine sediment is allowed to accumulate naturally. Similar to the WSP model (Supplementary Table 3), the model may remain stable across the simulation horizon. Therefore, the breakpoint function⁴⁸ is used to detect the onset of the shift, and the end of the shift is flagged once the fish population falls beneath 1% of the fish population recorded at the start of the simulation (Supplementary Fig. 10). The model exhibits fold bifurcation behaviour and hysteresis; for example, in Supplementary Fig. 11, whereby attempts to recover the collapsed fish population require the stressor (i.e. lake salinity, which is a proxy for lake sedimentation and tidal outlet closure) to be reversed back past the point that caused the original transition. The model is available on reasonable request from the authors of the original study²⁵.

Spatial Heterogeneity (SH) model

The SH model is an illustration of how spatial structure can affect the potential of systems to oscillate, particularly how stabilization can arise through spatial heterogeneity². The SH model is known to show Hopf bifurcations². The model uses predator-prey relationships to represent the interaction between zooplankton and algae co-existing within a lake but simplifies the spatial processes by considering zooplankton to be situated in one part of the lake, while algae are present throughout (Supplementary Fig. 12). Thus, in one compartment (A1) zooplankton graze the local population of algae, but the algae within the other compartment (A2) are predation free. The model experiments observe the shift to a state where the zooplankton are extirpated (Supplementary Fig. 13). Reference #2 provides a detailed description of the model’s original rationale and application. Here we show the reproducible Netlogo code (Supplementary Note 5) and the model parameters (Supplementary Table 7). To investigate the impact of the size of the ecosystem on the duration of the regime shift, we increased the carrying capacity of algae (K) by one, varying from 1 to 100 while maintaining constant parameters for all other variables (Supplementary Table 7). Using the ‘BehaviorSpace’ tool within Netlogo⁴⁷, every variation of this model was run for 10,000 time steps, resulting in 100 model runs. To investigate the impact of the system fluidity on the duration of the regime shift, we varied the fraction of volume exchanged between inside and outside (d; Supplementary Fig. 12) between 0 and 1 in increments of 0.01 (maintaining all other variables as constant; Supplementary Table 7). Every variation of this model was run for 10,000 time steps. This process resulted in 101 model runs. The SH model can be obtained from ref. ².

Identifying regime shift durations of modelled time series

The completed model runs detailed above were exported as comma-separated values and read into the statistical software R⁴³ for analyses. The University of Southampton supercomputer ‘Iridis 4’ was used to process the model outputs. To demark the start of the regime shifts for the WSP model that starts stable (Supplementary Fig. 6), we used the breakpoints function within the R-package ‘strucchange’⁴⁸. The breakpoint function is based upon finding significant deviations from stability in classical regression models, whereby the regression coefficients shift from one stable regime to another⁴⁸. We assume a priori that the number of statistically distinct time-series segments is equal to two: (1) pre-collapse state, (2) collapsed state, for the wolves, sheep and grass trends. Therefore, the breakpoint function searches for a single optimal breakpoint for each trend. Then for wolves and sheep, the end of the shift occurs once their respective abundances equal zero (Supplementary Fig. 7a,b), while the termination of the grass shift occurs once grass completely covers the system (Supplementary Fig. 7c). As detailed above, the Chilika model uses the same breakpoint strategy as the WSP model, with the breakpoint function detecting the shift from the first stable regime, and the end of the shift denoted by the first time step that the fish population is less than 1% of the original fish population. The breakpoint function is not required for the LC, GoL or SH model runs, as the models starts in an unstable state and so the start of the regime shift coincides with the first time step of the model. Therefore, in the LC model, the shift duration is equal to the number of time steps (from start) until all the system nodes have the same language state (Supplementary Fig. 8). In the GoL model, the shift duration is equal to the number of time steps (from start) until the model reaches a stable state in which either all cells are dead, or a stable mixed state has been maintained for 100 steps (Supplementary Fig. 9). Likewise, in the SH model, the shift duration is equal to the number of time steps (from start) until the first time step when the concentration of zooplankton equals zero (Supplementary Fig. 13). To produce the regression models from the modelled data (Fig. 3), the model runs that did not undergo shifts (as explained in this section) were omitted from analysis (Supplementary Table 9). Then, the log–log linear models were formulated, relating shift time to the variable of interest (Table 1). Variations in the rates of grass regrowth were accounted for within the WSP generalised linear models to assess the effect of the independent variable (Table 1) on shift duration for a given disturbance rate.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Source: Ecology - nature.com