Temperature-dependent competitive advantages of an allelopathic alga over non-allelopathic alga are altered by pollutants and initial algal abundance levels

Tested algae and culture conditions

Two freshwater microalgal species, P. subcapitata (strain CCAP 278/4) and C. vulgaris (strain AG40003), were acquired from the Culture Collection of Algae and Protozoa (CCAP, Scottish Marine Institute, UK) and the Korean Collection for Type Cultures (Korea Research Institute of Bioscience and Biotechnology, Korea), respectively. Both algal species were maintained separately in a 200 mL Erlenmeyer flask containing 100 mL of an algal growth medium (Supplementary Table S4), prepared according to United States Environment Protection Agency method⁵² 1003.0. The flasks were incubated in a static-temperature incubator at 20 ± 1 °C, for 16 h light/8 h dark photoperiod, and at 70 μmol photons m⁻² s⁻¹ using a cool white fluorescent light.

Experimental design

The three factors—copper exposure (three concentrations), initial abundance of the two algal species (three combinations), and temperature (five levels)—were tested to determine their effects on the competition between P. subcapitata and C. vulgaris. To measure the abundance of both algae over time in all experimental combinations, a full factorial experiment was designed. Thus, the experiments were conducted for 55 days with 45 combinations of the three factors until the growth and decline of the algal population were over. Nutrient and light conditions of the experiments were identical to the culture conditions and were not considered limiting factors during the experiments.

The exposure concentrations of copper were chosen to be lower than EC₅₀ (effective concentration giving a 50% reduction in the algal growth rate relative to the control) to ensure that copper does not severely inhibit the growth of the two algal species. According to Franklin et al.⁴⁴, 72 h EC₅₀ values of P. subcapitata and C. vulgaris at an initial abundance of 10⁵ cells mL⁻¹ at 27 °C are 17 and 16 μg L⁻¹, respectively. Considering that copper concentrations below EC₅₀ had a significant effect on algal competition in our previous study²², copper concentrations 5 and 10 μg L⁻¹ were chosen as the exposure levels for the present experiments. To prepare the copper-containing test media, a copper stock solution was made up by dissolving reagent grade copper (II) sulfate pentahydrate (CuSO₄·5H₂O, ≥99% purity, Sigma-Aldrich) in the algal growth medium, and then, the mixture was diluted with the medium to obtain the final exposure concentrations of 0 (control), 5, and 10 μg L⁻¹. The pH of the test medium was adjusted to 7.5 ± 0.1 with 0.1 M HCl or NaOH.

The algal growth experiments were carried out in a 100 mL glass beaker filled with 70 mL of the test medium along with three combinations of the initial abundance levels of the algae. The initial abundance levels of P. subcapitata and C. vulgaris in the three combinations were set up as follows: 2.5% and 10% (Combination A), 5% and 5% (Combination B), and 10% and 2.5% (Combination C) of the maximum abundance levels of each species in single culture (P. subcapitata: 5.0 × 10⁶ cells mL⁻¹, and C. vulgaris: 4.0 × 10⁷ cells mL⁻¹). To inoculate an algal amount corresponding to the determined initial abundance, P. subcapitata and C. vulgaris were sampled from steady-state algal cultures in which abundance was measured. The test beakers were sealed with parafilm (polyethylene) to prevent evaporation of the test solution and were placed separately in static-temperature incubators maintained at 15, 20, 25, 30, or 35 °C. To minimize the sedimentation and flocculation of the algal cells, the test beakers were manually agitated twice a day with the cover removed in the incubator. Five biological replicates were used for each of the 45 experimental conditions (n = 5).

During the 55 days of the experiment, the abundance of P. subcapitata and C. vulgaris was checked periodically (16 times total; until 3 weeks of exposure: every 1 to 4 days, thereafter: every 5 to 8 days). The abundance of algal cells in each beaker was measured five times by counting the algal cells in a sampled 5 μL algal suspension, using a hemocytometer (Marienfeld, Germany) under an optical microscope (E200; Nikon, Japan). Given that the two algal species have different shapes and sizes, the abundance of each species could be counted separately in a mixture under the microscope²².

It should be noted that no statistical analysis was performed to evaluate the effects of the tested factors on algal growth because the purpose of the experiments was to obtain experimental data for estimating the parameters of the model to be used in the simulations. Therefore, instead of hypothesis testing by means of the observed data, an evaluation of model performance was performed as described below.

Mathematical model and parameter estimation

To assess the influence of the copper exposure level, initial algal abundance, and temperature on the competition between the two algal species, the mathematical model previously developed by Kim et al.²² was utilized for the simulations. The model was employed to describe the dynamics of abundance levels of P. subcapitata and C. vulgaris during interference competition, including the allelopathic effect of C. vulgaris, which inhibits the growth of P. subcapitata by producing an allelochemical called chlorellin⁵³. The finding that chlorellin not only strongly inhibits the growth of P. subcapitata but also weakly inhibits the growth of C. vulgaris itself was taken into account in the model²⁶. Because the abundance levels of P. subcapitata and C. vulgaris could not reach an equilibrium owing to the strong interference competition between the two algal species via chlorellin²⁵, the model was designed to simulate transient dynamics of the algal abundance. The model is based on three ordinary differential equations representing algal abundance (X)^22,25, allelochemical concentration (p)⁵⁴, and habitat quality (S)²², as follows:

where the subscripts denote the following: a particular algal species, i; competitor species, j; initial abundance, 0; maximum abundance under the given conditions, m; and C. vulgaris, cv, which is a chlorellin-producing species. In Eq. (1), the changes in algal abundance, Ẋ_i, are determined by population growth, reflecting the temperature-dependent growth rate, μ_i(T), growth inhibition by chlorellin, exp(−r_ip), copper toxicity, 1 − (k_i(T)/(c_iX_i,0 + c_jX_j,0)), and habitat quality, S, as well as by population decline via temperature-dependent mortality, d_i(T). Because chlorellin has a much greater effect on the growth of P. subcapitata than C. vulgaris²⁶, the growth inhibition constant (r_i) is greater for P. subcapitata than for C. vulgaris. When the habitat quality reaches zero, the algal abundance decreases rapidly as population collapse, i.e., a_i(T)((X_i,m − X_i)/X_i,m), is added to the mortality. In Eq. (2), the concentration of chlorellin, p, has a linear relationship with the growth of C. vulgaris, Ẋ_cv, and α(T) as a temperature-dependent coefficient. In Eq. (3), habitat quality S starts from 1 and decreases gradually with the degradation of the habitat because of the depletion of nutrients and accumulation of toxic waste during the growth (Ẋ_in_i and Ẋ_jn_j) and metabolism (m_iX_i and m_jX_j) of the two algal species. S is conceptual representation of habitat quality of the coculture, is estimated by the observed data, and does not mean the actual concentration of nutrients or waste. Detailed descriptions of the parameters and units are given in Supplementary Table S5. More detailed descriptions of the model development and assumptions can be found in our previous study²².

The models described above were simulated using the Powersim studio (Powersim software AS, Norway) by the Euler integration method with 0.01 time-step in days. To calibrate the model using the observed data, the values of the parameters minimizing the sum of square error (the difference between the observed and simulated algal abundance) were estimated via the Powersim solver analysis tools. Five temperature-dependent parameters, i.e., the growth rate, μ_i(T), mortality, d_i(T), the abundance decrease rate, a_i(T), the chlorellin formation coefficient, α(T), and the copper toxicity coefficient, k_i(T), were estimated individually for each temperature condition. Other temperature-independent parameters, such as the habitat depletion rate (m_i and n_i), the inhibition constant (r_i), and the contribution rate toward copper bioavailability (c_i), were assumed (estimation) to have the same values at all temperatures.

The performance of the calibrated model was evaluated in three ways by means of PBIAS, the IoA, and ME^27,28. PBIAS measures the average tendency of the predicted data to be greater or less than the observed data (Eq. (4)). The optimal value of PBIAS is 0%, with a lower value indicating a more accurate prediction. The IoA (Eq. (5)) and ME (Eq. (6)) take a value between 0 and 1, and a higher value indicates that the model predictions better describe the observed data.

where n is the number of observed values, O_i is the i^th observed value, P_i is the i^th predicted value, and Ō is the mean of the observed values.

Simulations

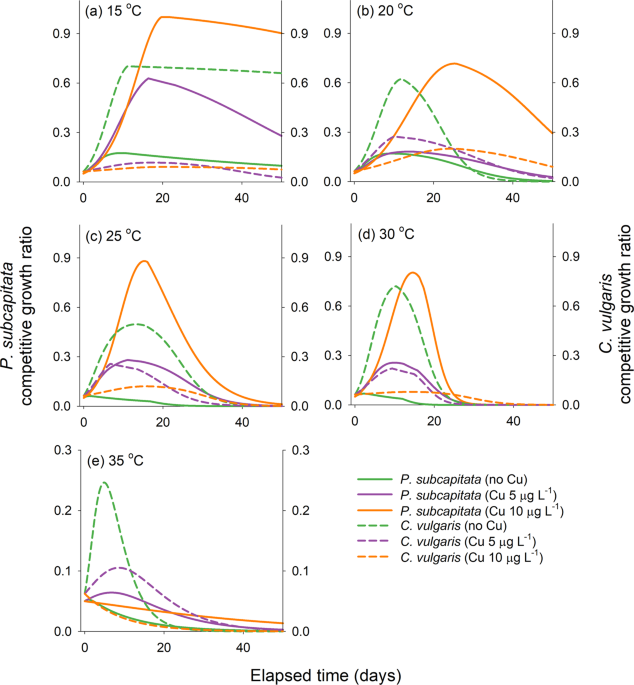
After the models were calibrated, a simulation analysis was performed to explore the effects of temperature, initial algal abundance, and copper exposure levels on interference competition between P. subcapitata (the non-allelopathic alga) and C. vulgaris (the allelopathic alga). To quantitatively describe the effect of each condition on the competition, two indices—competitive growth ratio and competitive dominance—were calculated from the predicted algal abundance levels. The competitive growth ratio is an indicator of how much the algal growth has been inhibited by the competitor and enables a sensible comparison when the difference in the carrying capacity between two species is substantial, as in the case of P. subcapitata and C. vulgaris⁵⁵. This index was calculated as the ratio of simulated abundance in the coculture to the optimal maximum abundance in the single culture that was already known (P. subcapitata: 5.0 × 10⁶ cells mL⁻¹, and C. vulgaris: 4.0 × 10⁷ cells mL⁻¹). The competitive dominance denotes the ratio of maximum abundance of each species in the coculture. This index, unlike the competitive growth ratio, does not indicate inhibition of the growth of allelopathic or non-allelopathic algae owing to the competition but shows which alga has an advantage under given conditions. The competitive dominance was calculated as the log₁₀-transformed ratio of the maximum abundance of C. vulgaris to that of P. subcapitata. To effectively identify the inhibition of algal growth by the interference competition, the log-transformed value of the ratio of the observed maximum abundance of P. subcapitata and C. vulgaris in the single culture was designated as a reference value.

Initial abundance is a broad concept that involves ratios and absolute values of one or more species. To thoroughly investigate the influence of the initial abundance in the simulation analysis, the initial abundance was classified as the initial abundance of the competitor, the initial abundance ratio of P. subcapitata and C. vulgaris, and absolute initial abundance (the sum of abundance levels of the two algal species). Their effects on the competition were sequentially analyzed through the simulation of the abundance of P. subcapitata and C. vulgaris in coculture in each initial abundance condition. First, to compare the effects of different temperatures on the competition between P. subcapitata and C. vulgaris, changes in abundance of the two algal species in the coculture were simulated at fixed initial abundance of both species at each copper exposure level and temperature. In this simulation, the initial abundance levels of P. subcapitata and C. vulgaris were fixed at 2.5 × 10⁵ and 2.5 × 10⁶ cells mL⁻¹, respectively (Simulation I in Supplementary Fig. S4), i.e., ~5% of their maximum abundance levels, and the abundance levels of each species were simulated for 55 d, the same experimental period at each temperature and copper exposure level. Second, a simulation was performed to assess the effect of changes in the initial abundance of their competitor on the competition outcome. In this simulation, the initial abundance of P. subcapitata and C. vulgaris was 2.5 × 10⁵ and 2.5 × 10⁶ cells mL⁻¹, respectively, as in Simulation I. The initial abundance of the competitors tested ranged from 2.0 × 10⁴ to 4.0 × 10⁵ cells mL⁻¹ for P. subcapitata and from 2.0 × 10⁵ to 4.0 × 10⁶ cells mL⁻¹ for C. vulgaris (Simulation II in Supplementary Fig. S4). Third, the changes in the competitive dominance in the coculture were simulated via changes in the initial abundance ratio under the given environmental conditions. The initial abundance ratios of C. vulgaris to P. subcapitata, ranging from 2.5 to 40, were tested by adjustment of the initial abundance of C. vulgaris and P. subcapitata from 1.0 × 10⁶ to 4.0 × 10⁶ and from 4.0 × 10⁵ to 1.0 × 10⁵ cells mL⁻¹, respectively (Simulation III in Supplementary Fig. S3). Lastly, the influence of absolute initial abundance on the competitive dominance was analyzed via adjustment of the initial P. subcapitata abundance from 2.5 × 10⁴ to 4.0 × 10⁵ cells mL⁻¹ and that of C. vulgaris from 2.5 × 10⁵ to 4.0 × 10⁶ cells mL⁻¹ (Simulation IV in Supplementary Fig. S4). The range of initial abundance levels of P. subcapitata and C. vulgaris covered by each simulation can be found in Supplementary Fig. S4.

To compare the effects of each type of initial abundance on the outcome of the algal competition, a local sensitivity analysis was performed. The sensitivity analysis was conducted via a disturbance method through changes in the initial value of a target variable (±20% of the default value), with calculation of the sensitivity (S) as follows^56,57:

where X is the maximum abundance ratio of C. vulgaris to P. subcapitata under given conditions, and Y is the target variable. The target variables were initial P. subcapitata abundance, initial C. vulgaris abundance, the initial abundance ratio, and absolute initial abundance. The default values of the initial abundance of P. subcapitata and C. vulgaris were 2.5 × 10⁵ and 2.5 × 10⁶ cells mL⁻¹, respectively, as in Simulation I. Sensitivity was analyzed for all combinations of temperatures and copper exposure levels.

Source: Ecology - nature.com